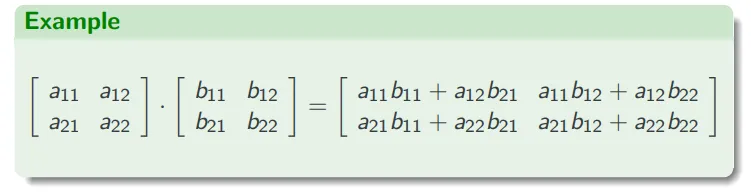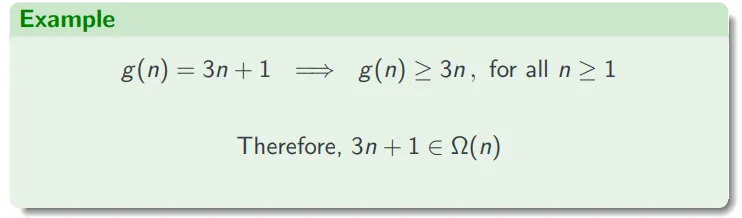Functions Recap
Functional Composition
Inverse Functions
Martrices
Introduction to Big-O Notation

函数性质重述 Functions Recap

二元关系的性质 Properties of Binary Relations

该部分详见 4.1 Relations - 二元关系的性质 Properties of Binary Relations

对于一个二元关系 $R \subseteq S \times T$ ，它可以有以下若干性质：

函数式（Fun） functional：对于每个 $S$ 中的元素 $s$ ，在关系 $R$ 中至多与一个 $T$ 中的元素 $t$ 关联。也就是说每个 $s$ 都至多映射到一个 $t$ 。
全域性（Tot） total：对于每个 $S$ 中的元素 $s$ ，在关系 $R$ 中至少与一个 $T$ 中的元素 $t$ 关联。也就是说每个 $s$ 都至少映射到一个 $t$ 。
单射（Inj） injective：对于每个 $T$ 中的元素 $t$ ，在关系 $R$ 中至多与一个 $S$ 中的元素 $s$ 关联。也就是说不同的 $s$ 映射到不同的 $t$ 。
满射（Sur） surjective：对于每个 $T$ 中的元素 $t$ ，在关系 $R$ 中至少与一个 $S$ 中的元素 $s$ 关联。也就是说 $T$ 中的每个元素都是某个 $s$ 的映射。
双射（Bij） bijective：关系 $R$ 同时满足单射和满射。也就是说， $S$ 到 $T$ 的映射是一对一的（每个 $s$ 只能映射到一个独特的 $t$ ），并且是覆盖的（ $T$ 中的每一个 $t$ 都被 $S$ 中的某个 $s$ 映射到）。

函数 Functions

一个函数 $f: S \times T$ ，本质上是一个满足了函数式（Fun）和全域性（Tot）的一个二元关系 $f \subseteq S \times T$ 。也就是说，对于所有的 $s \in S$ ，总能且只能找到一个 $t \in T$ ，使得 $(s,t) \in f$ 。

$f(s)$ ，指元素 $s$ 经过函数 $f$ 后对应的元素。
$T^S$ ，指所有从集合 $S$ 到集合 $T$ 的函数的集合。

一些术语符号 Symbols

术语

定义域（domain），包含所有可能的输入，即集合 $S$ 。
上域（co-domain），包含所有可能的输出，即集合 $T$ 。
像（image），即值域（range），是函数 $f$ 的实际所有输出，为 $T$ 的子集。

符号

定义域： $Dom(f)$
上域： $Codom(f)$
像： $Im(f)$ ，也可写作 $\{ f(x): x \in Dom(f) \}$

单射函数 Injective Functions

单射函数也称一对一函数，需要满足条件：每个元素 $s \in S$ 都映射到一个唯一的元素 $t \in T$ 上，并且不同的元素 $s$ 映射到 $T$ 中不同的元素。

注意：单射是一对一的，这意味着诸如绝对值（ $y = |x|$ ）这样的不是单射函数，因为不同的 $s$ 可能会映射到相同的 $t$ 上去。

满射函数 Surjective Functions

漫射函数也称“onto”，需要满足条件：如果函数的值域 $Im(f)$ 等于它的上域 $Codom(f)$ ，那么它就是满射的。

换句话说，如果它的上域中的每一个值都可以被函数通过定义域尽取到，那么我们可以说它就是满射的。

有限集上的函数 Functions on Finite Sets

对于一个有限集 $S$ ，以及一个从 $S$ 到 $S$ 的函数 $f: S → S$ ，单射和满射的性质是等价的。

函数复合 Functional Composition

定义 Definition

函数的复合指两个函数按照一定顺序执行，得到一个新的函数。

(g \circ f)(x)=g(f(x))

函数的复合是满足结合律的。即：

h \circ (g \circ f) = (h \circ g) \circ f

对于任何 $g: S \rightarrow T$ ，复合恒等式并不会改变函数 $g$ 。即：

id_S(x) = x \text{ for all } x \in S \\ g \circ id_S = g

函数自复合 Iteration of Functions

如果一个函数可以映射到它自己，即定义域与上域相等，那么这个函数就可以与自己复合。

f \circ f, f \circ f \circ f, ... \\ f^2, f^3, ...

逆函数 Inverse Functions

逆函数是一种特殊的函数，它可以将原函数 $f$ 的输出映射回到原函数的输入。只有当一个函数对于每个输入都有唯一的输出，并且每个输出都来自唯一的输入时（即函数是一一对应的），逆函数才存在。

当关系 $f^{\leftarrow}$ 是一个函数时，也可以被写作 $f^{-1}$ 。

只有当函数 $f$ 是双射时， $f^{-1}$ 才存在。
函数的逆 $f^{-1}$ 是撤销函数 $f$ 操作的过程。

逆函数的性质

如果函数 $f: S \rightarrow T$ ，并且 $f^{-1}$ 存在，那么：

f^{-1} \circ f = Id_S \\ f \circ f^{-1} = Id_T

如果函数 $f: S \rightarrow T$ 并且函数 $g: T \rightarrow S$ ，那么：

g \circ f = Id_S \\ f \circ g = Id_T

此时， $f^{-1}$ 存在，并且等于 $g$ 。

矩阵 Matrices

一个 $m \times n$ 矩阵是一个由m个水平行和n个垂直列构成的矩阵序列。

基本矩阵操作 Basic Matrix Operations

一个 $m \times n$ 矩阵 $A$ 的转置写作 $A^T$ ，是一个 $n \times m$ 的矩阵，原矩阵的第 $i$ 行 $j$ 列的元素，对应了其转置的第 $j$ 行 $i$ 列元素。

如果矩阵 $M$ 满足： $M = M^T$ ，那么该矩阵被称为对称矩阵。

矩阵相加 Matrix Sum

矩阵相加的结果，即让各个对应的元素分别相加，组成新的元素。只有行和列的数量完全相同的矩阵之间才可以使用加法。

A= \begin{bmatrix} 2 & -1 & 0 & 4 \\ 3 & 2 & -1 & 2 \\ 4 & 0 & 1 & 3 \end{bmatrix} \ \ \ B= \begin{bmatrix} 1 & 0 & 5 & 3 \\ 2 & 3 & -2 & 1 \\ 4 & -2 & 0 & 2 \end{bmatrix}

A+B= \begin{bmatrix} 3 & -1 & 5 & 7 \\ 5 & 5 & -3 & 3 \\ 8 & -2 & 1 & 5 \end{bmatrix}

矩阵加法之间可以使用交换律和结合律，即：

A + B = B + A \\ (A + B) + C = A + (B + C)

标量乘法 Scalar Product

给定一个 $m \times n$ 矩阵 $A = [a_{ij}]$ 和一个实数 $c$ ，标量乘积 $cA$ 是一个 $m \times n$ 矩阵，其第 $i$ 行 $j$ 列的元素是 $c \times a_{ij}$ 。

矩阵乘法 Matrix Product

给定一个 $m \times n$ 矩阵 $A=[a_{ij}]$ 和一个 $n \times p$ 矩阵 $B=[b_{jk}]$ ，它们的乘积是：

一个 $m \times p$ 的矩阵 $C = [c_{ik}]$ ，且：

c_{ik} = \sum^n_{j=1}a_{ij}b_{jk}

即：矩阵 $C$ 的第 $i$ 行 $k$ 列的元素是通过取 $A$ 的第 $i$ 行与 $B$ 的第 $k$ 列相应的元素乘积之和。

以下是一个2x2的矩阵乘积示例：

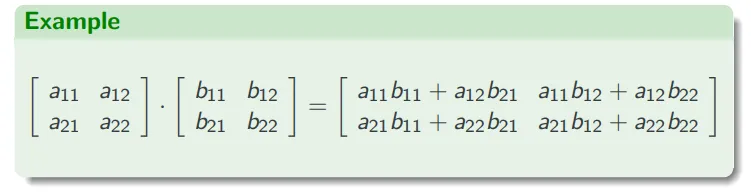
注意：

$A$ 的行数必须与 $B$ 的列数相同。
1xn的矩阵与nx1的矩阵的乘积，通常被称为两个n维向量（n-dimensional vector）的内积(inner product)/点积。
矩阵乘法不满足交换律。即： $AB \ne BA$ 。

大O符号简介 Introduction to Big-O Notation

“大O符号”是计算机科学中常用的一种数学记号，特别是在算法分析中用于表达算法的时间复杂度或空间复杂度。这个记号捕捉了函数随着输入规模增加的增长趋势。

假设有两个函数 $f$ 和 $g$ ，它们将自然数集 $N$ 映射到非负实数集 $R_{\ge 0}$ 。

如果存在某个常数 $n_0 \in N$ 和一个实数常数 $c \gt 0$ ，使得对所有的 $n \ge n_0$ ，都有 $g(n) \le c \cdot f(n)$ ，那么我们说 $g$ 是渐近小于等于 $f$ 的（或者说 $f$ 是 $g$ 的一个渐近上界）。

我们用 $O(f(n))$ 来表示所有渐近小于等于 $f$ 的函数 $g$ 的集合。

替代定义 Alternative Definition

如果 $f(n) \in O(g(n))$ ，当且仅当：

\lim_{n \rightarrow \infty} \frac{f(n)}{g(n)} < \infty

性质 Properties

给定如下几个函数：

f(n) \in O(g(n)) \\ g(n) \in O(h(n)) \\ j(n) \in O(k(n))

则有如下性质：

传递性

f(n) \in O(h(n))

加法性

f(n) + j(n) \in O(g(n) + k(n))

乘法性

f(n) \cdot j(n) \in O(g(n) \cdot k(n))

大Omega符号与渐近下界 Big-Omega Asymptotic Lower Bounds

假设有两个函数 $f$ 和 $g$ ，它们将自然数集 $N$ 映射到实数集 $R$ 。

如果存在某个常数 $n_0 \in N$ 和一个实数常数 $c \gt 0$ ，使得对所有的 $n \ge n_0$ ，都有 $g(n) \ge c \cdot f(n)$ ，那么我们说 $g$ 是渐近大于等于 $f$ 的（或者说 $f$ 是 $g$ 的一个渐近下界）。

我们用 $\Omega(f(n))$ 来表示所有渐近大于等于 $f$ 的函数 $g$ 的集合。

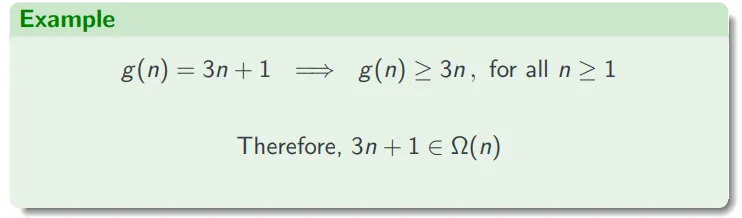
大Theta符号 Big-Theta Notation

两个函数 $f$ 和 $g$ 具有相同的增长阶（order of growth）或者是渐近等价的（asymptotically equivalent），如果它们以相同的方式随着输入大小的增加而增长。

如果存在某个常数 $n_0 \in N$ 和两个实数常数 $c,d \gt 0$ ，使得对所有的 $n \ge n_0$ ，都有 $c \cdot f(n) \le g(n) \le d \cdot f(n)$ ，那么我们说 $f$ 和 $g$ 具有相同的增长阶。

我们用 $\Theta(f(n))$ 来表示所有具有和 $f$ 相同增长阶的函数 $g$ 的集合。

关于界限：

如果 $g \in O(f)$ 或 $g \in \Omega(f)$ ，我们说 $f$ 是 $g$ 增长阶的上界或下界。
如果 $g \in \Theta(f)$ ，我们称之为紧确界（tight bound），因为它同时为 $g$ 的上界和下界。

性质

对称性

g \in \Theta(f) \leftarrow \rightarrow f \in \Theta(g)

由定义出发的包含性

\Theta(f(n)) \subseteq O(f(n)) \\ \Theta(f(n)) \subseteq \Omega(f(n))

由定义出发的交集

\Theta(f(n)) = O(f(n)) \cap \Omega(f(n))

逆反性

\text{if } g \in O(f), \text{ then } f \in \Omega(g)

观察值定理 Ovservations

对于所有的 $k, \epsilon > 0$ :
$O((log n)^k \subsetneq O(n^{\epsilon}))$
对数的任何多项式级别的增长都会小于任何正指数级别的增长。
$O(n^k) \subsetneq O((1+\epsilon)^n)$
任何多项式级别的增长都小于指数级别的增长。
所有的对数无论底数为何都具有相同的增长阶：
$O(log_2n) = O(log_3n) = ... = O(log_9n) = ...$
不同底数的指数函数具有不同的增长阶：
$O(r^n) \subsetneq O(s^n) \subsetneq O(t^n) \subsetneq ... \text{ for } r < s < t ...$
对于多项式函数也是类似的：
$O(n^k) \subsetneq O(n^l) \subsetneq O(n^m) \subsetneq ... \text{ for } k < l < m ...$

O(1)

$O(1)$ 表示常数时间复杂度，这意味着无论输入规模如何，执行时间（或复杂度）都保持不变。该复杂度通常是理想的，因为它意味着算法的运行时间或所需资源与输入大小无关。

从技术上讲，它可以是任何在两个常数 $c$ 和 $d$ 之间变化的函数，只要这个函数的值不依赖于输入规模 $n$ 。

目录