COMP9020 – Foundations of Computer Science

FINAL Exam – Term 3 2022

From Question 5 to Question 10

With my own solution (might be incorrect)

Question 5

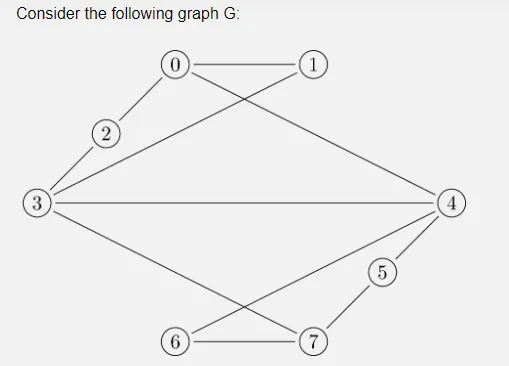
5.1

Question

Prove or disprove:

G has an Eulerian path

Here is the degree list for all of the vertices:

vertex 0: 3
vertex 1: 2
vertex 2: 2
vertex 3: 4
vertex 4: 4
vertex 5: 2
vertex 6: 2
vertex 7: 3

We could find that there are 2 vertices (0 and 7) whose degree is odd. This could prove that there is an Eulerian path in G.

For example:

0 → 2 → 3 → 1 → 0 → 4 → 5 → 7 → 6 → 4 → 3 → 7

5.2

Question

Prove or disprove:

G has a Hamiltonian cycle

If it has a Hamiltonian cycle, it means that no matter which vertex I start, I could find a cycle. Because this cycle should get every vertex.

Divide these vertices into 2 subsets: {0, 1, 2, 3} and {4, 5, 6, 7}. Edges (0, 4), (3, 4) and (3, 7) are linking these 2 subsets.

Set start point at vertex 1, and we could go to vertex 0 or vertex 3.

If we go to vertex 0, we could go to vertex 2 or vertex 4 for next step.

If we go to vertex 2, we must go to vertex 3 for next step, but it means that we could not come back from {4, 5, 6, 7} because we should use vertex 0 or vertex 3 to go back and get vertex 1 at the last step.

So we should return, and go to vertex 4 when we are at vertex 0. However, after a trip in {4, 5, 6, 7}, we can only go back by vertex 3, and then we must choose to go to vertex 2 and get vertex 0. This is also a bad path.

So we return again, and go to vertex 3 when we are at vertex 1. However, it is same when we come back from {4, 5, 6, 7}. we could only choose vertex 0 to come back, but we have to go to vertex 2 and reach the vertex 3 in the end.

In conclusion, after the path finding, we could prove that this graph does not have a Hamiltonian cycle.

5.3

Question

Prove or disprove:

The chromatic number of G is equal to the clique number of G. That is, χ(G) = κ(G).

The clique number should be the vertex number of the smallest complete sub-graph in G.

In graph G, we could only find 2-clique (an edge and 2 vertices at 2 sides). There is not any tri-angle (3-complete graph) in G. Therefore, $κ(G) = 2$ .

Set vertex 0 in BLACK. And we could find that:

vertex 0: BLACK
vertex 1: WHITE
vertex 2: WHITE
vertex 3: BLACK
vertex 4: WHITE
vertex 5: BLACK
vertex 6: BLACK
vertex 7: WHITE

2 colors(black & white) could color graph G. Therefore, $χ(G) = 2$ .

We could prove that:

χ(G) = κ(G)

Question 6

Let Σ = {a,b,c}

Consider the function del:Σ* → Σ* which works as follows:

For w∈Σ*, del(w) is the word that results from removing all c's from w.

For example:

del(aabbcc) = aabb
del(ccbbaacc) = bbaa
del(bacabc) = baba
del(cccc) = λ
del(bbbb) = bbbb

6.1

Question

Give a recursive definition of the function del:Σ* → Σ*

$del(\lambda) = \lambda$
$del(cx) = del(x)$
$del(mx) = m + del(x)$ if $m \in {a,b}$

Python
def del(w):
    if not w:
        return w
    if w[0] == 'c':
        return del(w[1:])
    else:
        return w[0] + del(w[1:])

6.2

Question

Let Σ={a,b,c}.

For w∈Σ*, let P(w) be the proposition that:

For all $v \in Σ^*$ : $del(wv) = del(w)del(v)$

Prove, using your definition of del from part (a), that P(w) holds for all w∈Σ*.

When $w = \lambda$ , P(w) could be:

For all $v \in Σ^*$ : $del(v) = del(v)$

It is true.

When $w = w_1w_2...w_k$ ,

Set: $Σ' = {a,b}$ , and single element $w_i$ could be: $Σ'^*c^*Σ'^*$ .

$del(wv) = del((Σ'^*c^*Σ'^*)^*v) = (Σ'^*Σ'^*)^*del(v)$

In addition, $del(w) = (Σ'^*Σ'^*)^*$

Therefore, we could prove that:

P(w) holds for all w∈Σ*.

Question 7

Consider the following two pieces of code.

The first moves the minimum element of a list to its head


extractMin(L):	 
    if length(L) <= 1: return L
 	 
    x = L.head	 
    L2 = extractMin(L.next)	 
    if x < L2.head:	 
        return L	 
    else:	 
        L3 = (x, L2.next)	 
        return (L2.head, L3)

The second sorts a list by repeatedly extracting the minimum element using extractMin


mySort(L):	 
    i = 0	 
    L2 = empty
    L3 = L	 
 	 
    while i < length(L):	 
        L3 = extractMin(L3) 
        L2 = (L3.head, L2)	 
        L3 = L3.next	 
        i = i+1	 
 	 
    return L2

7.1

Question

Find an asymptotic upper bound for T(n): the running time of the worst-case of extractMin(L) where L is a list with n elements.

You may assume that creating a list is an elementary operation, as is checking the length of L.

The worst case is that:

for every element in position i, it is the least element compared with all elements before. function should move n-i times to make it to the top of this list.

T(n) = T(n-1) + O(n)

And the sum is:

T(n) = O(n) + O(n-1) + ... + O(1) = O(\frac{n(n+1)}{2}) \\ T(n) = O(n^2)

7.2

Question

Find an asymptotic upper bound for R(n): the running time of the worst-case of mySort(L) where L is a list of n elements.

You may assume that creating a list is an elementary operation, as is checking the length of L. You may assume the running time of extractMin on a list of length n is T(n) [if not previously calculated].

We have proved that the worst-case of extractMin(L) is: $O(n^2)$ .

And for mySort(L), it use $O(n)$ time to execute while command, and every loop it executes extractMin(L) to calculate the least element.

Therefore, the worst upper bould for $R(n) = O(n^2 \times n) = O(n^3)$ .

Question 8

A spaceship is full of crewmates and imposters. Crewmates always tell the truth, and imposters always lie. Everyone is either a crewmate or an imposter. Three members of the spaceship, Red, Green and Blue, make the following statements:

Red: Blue is not an imposter
Green: At least one of Blue or Green is a crewmate
Blue: Green is an imposter

You would like to know if at least one of Red or Blue is an imposter.

8.1

Question

Explain how this problem can be modelled as a problem in Propositional Logic. In particular, clearly define:

The propositional variables you are using and what propositions they represent
Any formulas that are appropriate, and what propositions they represent
The Propositional Logic problem to be solved

We could define that:

$R$ ：Red is crewmate
$G$ : Green is crewmate
$B$ : Blue is crewmate

According to the statement of Red, if Red is crewmate, we could find that Blue is crewmate. If Red is not crewmate, Blue is not crewmate. That means:

R \rightarrow B\\ \neg R \rightarrow \neg B \\ R \leftrightarrow B

According to the statement of Green, there is at least one crewmate between Green and Blue.

\neg B \vee \neg G

According to the statement of Blue, if Green is a crewmate, Blue is an imposter; if Green is an imposter, we could find that this statement is true, and Blue is crewmate. That means:

\neg G \rightarrow B \\ G \rightarrow \neg B \\ \neg G \leftrightarrow B

8.2

Question

Using the Propositional Logic model of part (a), solve the given problem.

We have that:

$R \leftrightarrow B$
$\neg G \leftrightarrow B$
$\neg B \vee \neg G$

According to first two statement, we could find that:

$R \leftrightarrow \neg G$

Assum: R is true.

According to $R \leftrightarrow B$ , B is true.
According to $R \leftrightarrow \neg G$ , G is false.
$\neg B \vee \neg G$ is true. However, it should be false because Green is imposter.

Assum: R is false.

According to $R \leftrightarrow B$ , B is false.
According to $R \leftrightarrow \neg G$ , G is true.
$\neg B \vee \neg G$ is true.

Therefore, there is a solution for this spaceship:

Red is imposter
Green is crewmate
Blue is imposter

Question 9

9.1

Question

Suppose you have:

x indistinguishable red balls
y indistinguishable blue balls
z indistinguishable green balls

Show that there are:

\binom{x+y+z}{z}\binom{x+y}{y}

ways of placing the balls into x+y+z distinguishable boxes with exactly one ball per box.

We could use 3 steps to place all the balls:

select z empty boxes and place all of the green balls.
select y empty boxes and place all of the blue balls.
place all of the red balls into the rest boxes.

Because every ball is indistinguishable, we do not need to consider the order of placing between same color balls.

For the first step, we have $T_1$ ways:

T_1 = C_{x+y+z}^{z} = \binom{x+y+z}{z}

For the second step, we have $T_2$ ways:

T_2 = C_{x+y}^{y} = \binom{x+y}{y}

And the last step do not need any extra calcuation. Because after step 1 and step 2, there is just one option for step 3 to put balls.

In addition, the selection in step 1 could effect selection in step 2. Because every box is distinguishable. Therefore, every selection is unique.

So we could prove that the way of placing balls are:

T_1 \times T_2 = \binom{x+y+z}{z}\binom{x+y}{y}

9.2

Question

Show that for all x,y,z ∈ ℕ:

\binom{x+y+z}{z}\binom{x+y}{y} = \binom{x+y+z}{x}\binom{y+z}{y}

If we have the same question in 9.1, we could change the steps in another way:

select x empty boxes and place all of the red balls.
select y empty boxes and place all of the blue balls.
place all of the green balls into the rest boxes.

Because every ball is indistinguishable, we do not need to consider the order of placing between same color balls.

For the first step, we have $T_3$ ways:

T_3 = C_{x+y+z}^{x} = \binom{x+y+z}{x}

For the second step, we have $T_4$ ways:

T_4 = C_{y+z}^{y} = \binom{y+z}{y}

And the last step do not need any extra calcuation. Because after step 1 and step 2, there is just one option for step 3 to put balls.

In addition, the selection in step 1 could effect selection in step 2. Because every box is distinguishable. Therefore, every selection is unique.

So we could prove that the way of placing balls are:

T_3 \times T_4 = \binom{x+y+z}{x}\binom{y+z}{y}

We use different ways to solve same question, and the result should be equal.

Therefore, it should be:

T = T_1 \times T_2 = T_3 \times T_4

It means that:

\binom{x+y+z}{z}\binom{x+y}{y} = \binom{x+y+z}{x}\binom{y+z}{y}

Question 10

Let $Σ = \{a,b,c\}$

Let $p(k, n)$ be the probability that a word (over Σ) of length n, drawn uniformly at random from the set of all words of length n, contains exactly k c's.

10.1

Question

What is p(0,n)?

Justify your answer

For every character in a n-word, the possibility that it is not 'c' is $\frac{2}{3}$ .

Therefore, $p(0,n) = (\frac{2}{3})^n$ .

10.2

Question

What is p(n,n)?

Justify your answer

For every character in a n-word, the possibility that it is 'c' is $\frac{1}{3}$ .

Therefore, $p(n,n) = (\frac{1}{3})^n$ .

10.3

Question

Give, with justification, an expression for p(k,n), either:

in terms of combinatorial functions, or
recursively, in terms of p(k', n') where k'≤k and n'≤n

We use combinatorial functions to solve this question.

For a n-word, we should select k characters to set 'c', and other characters are not 'c'.

Therefore, we could find that:

p(k,n) = \binom{n}{k} \times (\frac{1}{3})^k \times 1 \times (\frac{2}{3})^{n-k}

It is:

p(k,n) = \binom{n}{k} \times \frac{2^{n-k}}{3^k}

By the way, the recursive way is:

p(k,n) = \frac{1}{3}p(k-1,n-1) + \frac{2}{3}p(k, n-1)

10.4

Question

What is the expected number of c's in a word of length n, drawn uniformly at random from the set of all words (over Σ) of length n?

For every character, $c_i$ , in n-word, the possibility of 'c', $p_i$ , is $\frac{1}{3}$ .

The expected number of c is:

\sum_{i=1}^n p_i \times length(w_i) = \frac{1}{3} \times 1 + \frac{1}{3} \times 1 ... + \frac{1}{3} \times 1 = \frac{n}{3}

目录

Question 5

5.1

5.2

5.3

Question 6

6.1

6.2

Question 7

7.1

7.2

Question 8

8.1

8.2

Question 9

9.1

9.2

Question 10

10.1

10.2

10.3

10.4