Lecture 3: Sets and Formal Languages

Introduction to Sets
Defining Sets
Set Operations
Formal Languages

集合简介 Introduction to Sets

定义 Definition

A set is a collection of objects (elements). If x is an element of A, we write x ∈ A.

集合内的元素没有顺序，也没有重复性。
单个元素和单元素集合本身需要进行区分。即： $a\ne\{a\}$ 。
空集的表示： $\empty = \{\}$ ，即没有元素。
该集是非空的： $\{\empty\}$ ，它有一个元素： $\empty$ 。

The most set is universe, $U$ .
Not all "well-defined" universes are possoble.
- No "set of all sets" (Cantor's paradox)
- No "sets which do not contain themselves" (Russel's paradox)

康托尔悖论

Cantor's Paradox 是一个与集合论有关的悖论，由数学家格奥尔格·康托尔（Georg Cantor）提出。它揭示了“所有集合的集合”这一概念在朴素集合论中的自我矛盾性。这个悖论可以这样解释：

朴素集合论中的集合：在朴素集合论中，一个集合可以被理解为任意对象的一个整体，其中的对象称为该集合的元素。集合可以包含其他集合作为其元素。

“所有集合的集合”：如果我们尝试构建一个包含所有集合作为其元素的集合，我们可以称之为“全集”（或“所有集合的集合”）。

Cantor 的对角线论证：康托尔发展了一种称为“对角线论证”的方法，用以证明实数集合的势（或大小）大于自然数集合的势。这个方法也可以用来展示“所有集合的集合”不能存在。

首先，假设存在一个“所有集合的集合”S。然后，考虑所有从S到其自身的可能子集。根据康托尔的对角线论证，可以证明S的所有子集的集合的势（大小）必然大于S本身的势。这意味着S不能包含所有可能的集合，因为它至少缺少了一些子集。悖论的核心：悖论在于，如果我们试图构建一个包含一切可能集合的“全集”，那么根据对角线论证，这个“全集”必须比自身还要大，这是不可能的。这表明在朴素集合论中无法构建一个同时包含所有集合的集合。

解决方案：为了解决这个悖论以及集合论中的其他类似问题，数学家们发展了公理化集合论（如ZFC集合论），在这些理论框架中，通过引入公理来限制集合的构造，从而避免了这类悖论的出现。

Cantor's Paradox 揭示了朴素集合论的局限性，促使数学家寻求更加严格和精细的理论框架来处理集合及其相关概念。

罗素悖论

罗素悖论（Russell's Paradox）是由英国哲学家和数学家伯特兰·罗素（Bertrand Russell）提出的一个著名逻辑学和集合论中的悖论。它直接挑战了朴素集合论的基本假设，并促进了集合论的公理化。罗素悖论可以这样解释：

朴素集合论的背景：在朴素集合论中，一个集合可以定义为满足某种特定性质的所有对象的汇总。理论上，任何性质都可以定义一个集合。

自我包含的集合：如果一个集合作为自己的元素，则称这个集合为自我包含的。例如，集合“所有集合”的集合是自我包含的，因为它本身是一个集合，所以它包含自己。

罗素悖论的构造：罗素考虑了这样一个集合R，R包含所有不包含自己作为元素的集合。换句话说，如果一个集合x不是自己的元素，那么x就是R的一个元素。

悖论的发生：

现在我们询问：集合R是否包含自己？有两种可能性：如果R包含自己，根据R的定义，它只应该包含那些不包含自己的集合。因此，如果R包含自己，它就违背了自己的定义。如果R不包含自己，根据R的定义，它应该包含所有不包含自己的集合，包括R本身。因此，如果R不包含自己，根据定义，它应该包含自己。这两种情况都导致矛盾，因此无法确定R是否包含自己。悖论的意义：罗素悖论展示了朴素集合论中关于集合可以由任意性质定义的假设的问题。它说明了需要更加严格的原则来避免这类逻辑悖论。

解决方案：为了解决罗素悖论以及其他相关悖论，数学家发展了新的集合论体系，如Zermelo-Fraenkel集合论（ZF）和带有选择公理的Zermelo-Fraenkel集合论（ZFC）。这些公理化集合论通过限制集合的构建方式，避免了像罗素悖论这样的自相矛盾。

罗素悖论不仅在数学史上占有重要位置，也对逻辑学、哲学以及数学的基础研究产生了深远影响。通过引入更加严格的集合论公理，数学家能够构建一个更加一致和稳固的数学基础。

子集 Subsets

如果集合 $S$ 的所有元素都是集合 $T$ 的元素，我们说 $S$ 是 $T$ 的子集，写作 $S \subseteq T$ 。

$S \subseteq T$ 包含情况： $S=T$
$S \subset T$ 包含情况： $S \ne T$
对于所有的集合 $S$ ，均有 $\empty \subseteq S$
对于所有集合 $S$ ，均有 $S \subseteq U$
$N_{>0} \sub N \sub Z \sub Q \sub R$
集合的一个元素，和集合的一个子集，不是一个东西。

a \in \{a,b\}, a \nsubseteq \{a,b\}; \\ \{a\} \subseteq \{a,b\}, \{a\} \notin\{a,b\}

定义集合 Defining sets

显式枚举 Enum

直接对集合内的元素进行枚举，以得到每一个元素，从而定义一个集合。

下定义 Defining

使用多项式、不等式等方式为集合元素下定义，从而定义一个集合。

特殊形式：Intervals

使用符号直接划定范围，该范围可以视为一个集合。

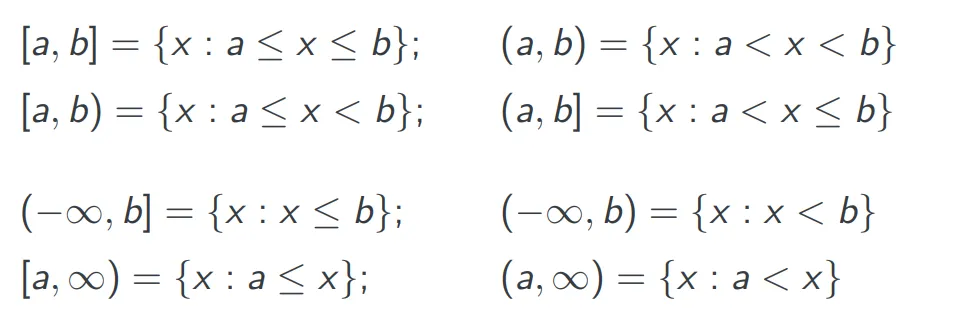
从已有集合中构造

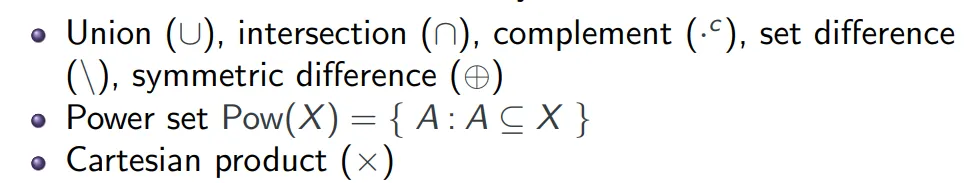
集合操作 Set Operations

并集 union：

A \cup B = \{x:x \in A \ or\ x \in B\}

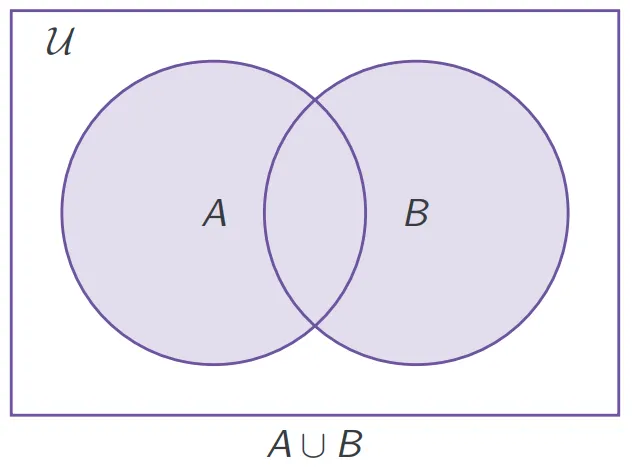
交集 intersection：

A \cap B = \{x:x \in A \ and\ x \in B\}

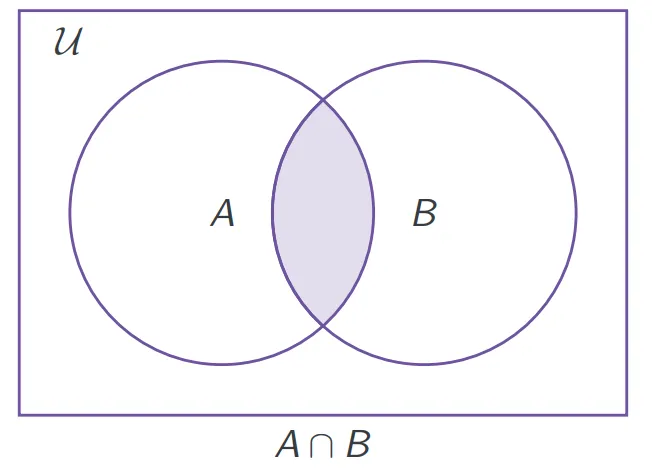
补集 complement：

A^C=\{x:x\in U \ and\ x\notin A\}

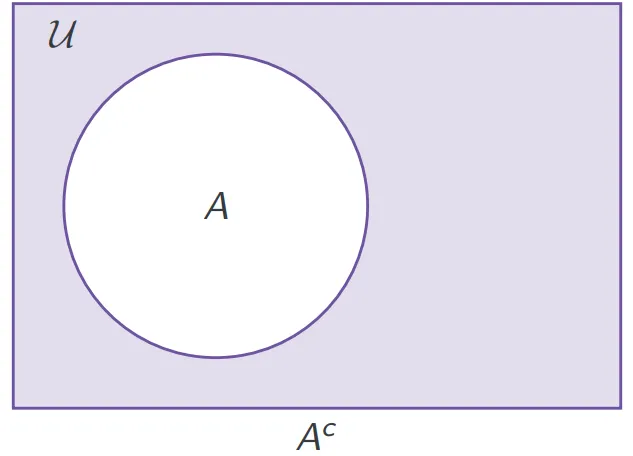
不相交 disjoint：

A \cap B = \empty

集合差 set difference：

A \backslash B = A \cap B^C \\ \text{A but not B}

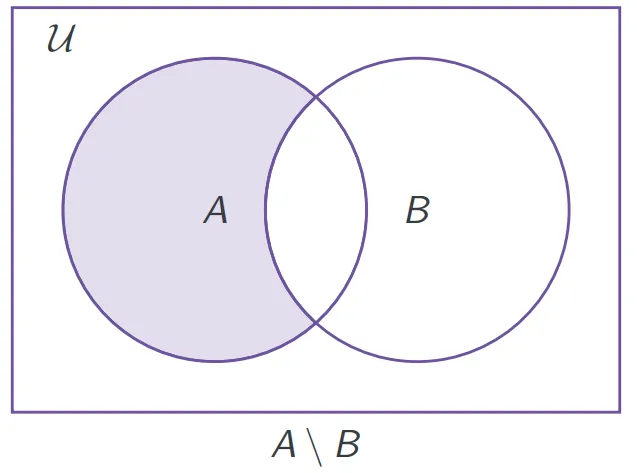
对称差 symmetric difference：

表示两集合中各自独有的元素的集合。

A \oplus B = ( A \backslash B ) \cup ( B \backslash A ) \\ \text{A and not B, or B and not A} \\ \text{A xor B}

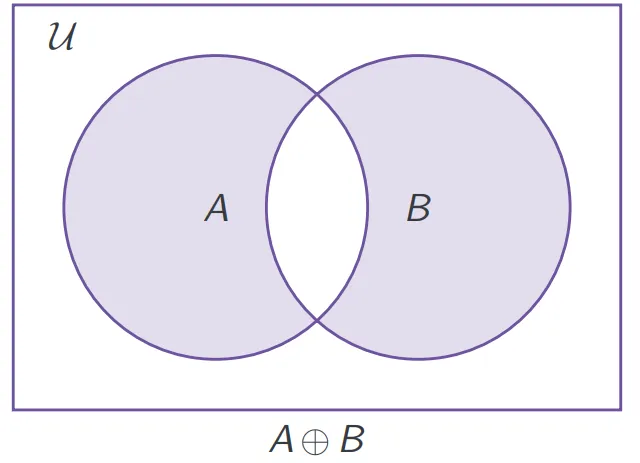
集合操作与子集 Set Operations and Subset

A \cup B = B \ \text{iff} \ A \cap B = A \ \text{iff} \ A \subseteq B

A \oplus A = \empty \\ A \oplus \empty = A

幂集 Power Set

幂集，指一个集合的所有子集，包括了空集和它本身。

基数 Cardinality

指集合中元素的数量。它是用来衡量集合大小的属性。

|X| = \#(X) = card(X)

以此，有如下定理：

一个集合的子集数量等于其2的基数幂。

|Pow(X)|=2^{|X|}

另有：

|[m,n]|=n-m+1,\ m<=n,\ m,n \in Z

笛卡尔积 Cartesian Product

笛卡尔积（Cartesian Product）是集合论中的一个运算，用来生成由所有可能的有序对组成的集合。给定两个集合 A 和 B，它们的笛卡尔积是指形如 (a, b) 的所有有序对的集合，其中 a 属于集合 A，b 属于集合 B。

S \times T=\{(s,t): s \in S, t \in T\} \\

笛卡尔积不支持乘法交换律和乘法结合律。

A \times B \ne B \times A \\ A \times (B \times C) \ne (A \times B) \times C

如果有n个集合，那么它们的笛卡尔积的结果就是所有的有序n元组构成的集合。每个n元组的第i个元素来自集合 $S_i$ 。

\times^n_{i=1}S_i=\{(s_1,...,s_n):s_k \in S_k, \ 1 \le k \le n\} \\ S^2=S \times S \\ S^n = \times_1^nS

有以下基本事实：

\empty \times S=\empty \\ |S \times T| = |S| * |T| \\ |\times^n_{i=1}S_i|= \prod^n_{i=1}|S_i|

注意： $\Pi_n^1$ 是乘积符号（大写的希腊字母Pi），代表累乘。

形式化语言 Formal Languages

形式化语言（Formal Language）在数学、逻辑和计算机科学中指的是一套有严格规定的符号和字符串集合，这些字符串是根据某个形式系统的规则从一个字母表中构建的。在形式化语言中，语法规则严格定义了哪些字符串是有效的，哪些不是。这种语言通常用于表达数学、计算机程序的命令和结构以及其他逻辑系统。

字母表 Alphabet

一个字母表是一个基本符号或字符的集合，这些符号或字符本身没有预定义的含义。（有限，非空）

字符 Word

字母表中的有限字符序列（字符串）。可以为空，表示为 $λ$ （Lambda）。

Concatenation：连接。

词集 Set of words

通常指的是由特定字母表中的字符构成的所有可能字符串的集合。

有以下事实：

\Sigma^1=\Sigma \\ \\ \Sigma^*=\Sigma^0 \cup \Sigma^1 \cup \Sigma^2 \cup ...; \ \ \Sigma^{\le n}=\bigcup^n_{i=0}\Sigma^i \\ \Sigma^+=\Sigma^1 \cup \Sigma^2 \cup ...=\Sigma^* \backslash \{\lambda\}

语言 Languages

集合操作的形式化语言 Set Operations for Languages

字符连接

直接并列写出即可，顺序不可更换。

XY=\{xy: x\in X \ and \ y \in Y\}

连续集合内的字符

可以用指数符号与星号代指数量。

X^0=\{\lambda\} \\ X^{i+1}=XX^i \\ X^*=X^0 \cup X^1 \cup X^2 \cup ...

目录