• Elementary Discrete Probability
• Independence
• Infinite Sample Spaces
• Recursive Probability Computations
• Conditional Probability
• Independence, revisited

初等离散概率 ELementary Discrete Probability

初等概率 Elementary Probability

概念定义

1. 样本空间（Sample Space）：包含所有可能结果的集合，每一个元素代表一个可能的结果。

2. 事件（Event）：是结果的集合，是样本空间的子集。
3. 概率分布（Probability Distribution）：是一个函数 $P: Pow(Ω)→ ℝ$，满足：

基本事实

• $P(∅) = 0$，意味着一个不可能事件的概率是0。
• $P(Eᶜ) = 1 - P(E)$，其中 $Eᶜ$ 是 $E$ 的补事件，这表示事件 $E$ 不发生的概率。

均匀分布 Uniform Distribution

在均匀概率分布中，样本空间Ω中的每个结果ωᵢ都是等可能的。具体地，对于样本空间Ω中的每个结果ω₁, ω₂, ..., ωₙ，它们发生的概率相同，用概率论的术语表示为：

这称为样本空间Ω上的均匀概率分布。在这种分布下，每个单独事件发生的概率是相等的，这是一个在理想化的公平游戏或者是理想情况下的随机实验中常见的分布。

通过计数计算概率 Computing Probabilities by Counting

在没有其他资料的情况下，"随机选择"这个表述通常意味着"根据均匀分布"进行选择。这意味着每个可能的结果都有相同的概率发生。

大多数计数规则可以直接转换为关于均匀分布的概率。这是因为在均匀分布下，概率直接与样本空间中特定事件的数量相关联。

组合事件 Combining Events

通过组合简单事件来构造复杂事件：

• 事件A和事件B同时发生：使用交集符号表示，即 $A \cap B$。
• 事件A或事件B发生（至少一个发生）：使用并集符号表示，即 $A \cup B$。
• 事件A不发生：使用补集符号表示，即 $\Omega \backslash A$。
• 事件A发生后事件B发生：这通常涉及条件概率或序列事件，可能用其他概率规则来描述。

前三种构造涉及到来自同一样本空间的事件，而最后一种可能涉及来自不同样本空间的事件（例如先掷骰子再抛硬币）。

独立事件 Independence

统一不同集合的结果 Unifying sets of outcomes

• 抛硬币的样本空间可以表示为 $\Omega_1 = \{heads, tails\}$
• 掷骰子的样本空间可以表示为 $\Omega_2 = \{1, 2, 3, 4, 5, 6\}$

这两个活动可以结合起来创建一个新的样本空间 $\Omega = \Omega_1 \times \Omega_2$，包括所有可能的组合。

这种方法也可以用来建模结果序列。这意味着它不仅仅用于单次事件，还可以用于表示一系列连续事件的所有可能结果。这种方法在多阶段实验中非常有用，其中每个阶段都可能有不同的结果集。

乘积分布 Product Distribution

表示在一个维度上的事件的概率不会受到其他维度上结果的影响。这个性质是独立性的体现，它是说在乘积空间中的事件发生的概率是各自独立事件概率的乘积。

独立性 Independence

非正式定义

事件被认为是独立的，如果一个事件的结果不影响另一个事件的结果。

正式定义

如果两个事件，事件A和事件B，同时发生的概率等于各自发生概率的乘积，那么它们被称为（随机）独立的（记作 $A⊥B$ ）。

除非另有说明，当我们在统一事件时（在适当的情况下），我们假设事件是独立的。这个假设是为了简化问题分析，因为在实际应用中，事件的独立性往往需要明确指出或由问题的背景决定。

全独立性与成对独立性

• 全独立性 Full Independence：所有事件之间都相互独立，它们同时发生的概率等于它们各自发生概率的乘积。
• 成对独立性 Pairwise Independence：相对更弱，它只要求每对事件之间相互独立，而不是要求所有事件之间。

例如，考虑两次抛硬币的实验：

1. 事件A：第一次抛硬币得到正面（H）
2. 事件B：第二次抛硬币得到正面（H）
3. 事件C：两次抛硬币中恰好一次得到正面（H）

虽然A和B是独立的，A和C是独立的，B和C也是独立的（即所有的成对事件独立，$P(A) = P(B) = P(C) = \frac{1}{2}$， 且 $P(A∩B) = P(A∩C) = P(B∩C) = \frac{1}{4}$），但事件A、B和C并不是全独立的，因为 $P(A∩B∩C) = 0 \ne P(A)·P(B)·P(C)$。

这个例子说明了成对独立性并不总是蕴含全独立性。而且还可以构造一组n个事件，其中任意k个是独立的，但任意k+1个就不是独立的（$k < n$）。

二项分布 Binomial Distribution

在一系列的n个独立试验中，每次试验成功的概率为p，那么恰好有k次成功的概率可以用下面的公式来表示：

这种概率分布模式被称为二项分布。二项分布是离散概率分布的一个重要例子，常用于描述固定数量独立试验中成功次数的概率。这里的“成功”可以指任何感兴趣的二分结果，例如抛硬币得到正面或者负面，测试结果为阳性或阴性等。

无穷样本空间 Infinite Sample Spaces

在连续空间中（例如实数 ℝ）：

• 概率分布被视为度量（measures）。
• 求和操作通过积分来完成。
• 非零概率适用于范围而不是单点。
• 单个事件的概率是0，但这并不意味着该事件是不可能的，因为在连续空间中，有无限多个可能的结果。

在离散空间中（例如自然数 ℕ）：

• 概率为0确实意味着某个事件是不可能的。
• 不存在均匀分布，因为不能给无限个事件赋予相同的非零概率，使它们的总和为1。
• 非均匀分布是存在的。例如，可以有一个分布，其中 $P(0) = 1$ 而所有 $P(n) = 0（n > 0）$，或者分布 $P(0) = 0, P(n) = \frac{1}{2^n} (n > 0)$。
• 在某些情况下，如果合理的话，可以考虑极限概率。

递归概率计算 Recursive Probability Computations

• H: Head，正面。
• T: Tail，反面。

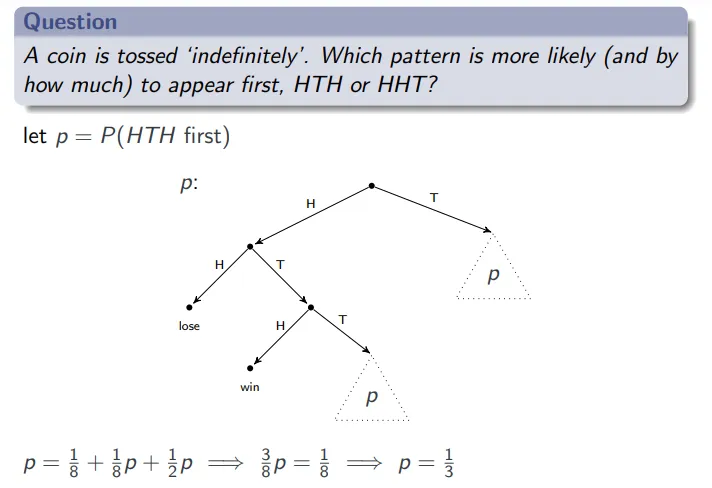
大多数概率和统计问题没有简洁优雅的解决方案。因此，使用计算机进行精确计算或近似模拟变得必不可少。然而，递归的使用简化了这样的计算，或者很多时候，使这样的计算成为可能。递归是指自己调用自己的函数，这在处理复杂的概率计算时特别有用，尤其是在可以将问题分解成更小、更简单的子问题时。

条件概率 Conditional Probability

事件E在事件S已经发生的条件下发生的概率，记为 $P(E|S)$，定义为：

条件概率只有在 $P(S) \ne 0$ 时才有定义。

基本事实

• $A \subseteq B \rightarrow P(A|B) \le P(A)$：在事件B发生的条件下事件A发生的概率至少和A无条件发生的概率一样大。
• $A \subseteq B \rightarrow P(B|A) =1$：如果事件A发生了，那么事件B肯定发生。
• $P(A \cap B | B) = P(A | B)$
• $A \ne \empty \rightarrow P(\empty | A) = 0$：对于非空事件A，在事件A发生的条件下，不可能事件发生的概率是0。
• $P(A|\Omega) = P(A)$：在整个样本空间发生的条件下事件A发生的概率就是事件A本身的概率。
• $P(A^C|B) = 1-P(A|B)$：事件A在B发生的条件下不发生的概率等于1减去A在B发生的条件下发生的概率。

独立性与条件概率

假设事件A和事件B时随即独立的，即：

如果 $P(A) \ne 0, P(B) \ne 0$，那么下列陈述完全等价：

• $P(A \cap B) = P(A)P(B)$
• $P(A|B) = P(A)$
• $P(B|A) = P(B)$
• $P(A^C|B) = P(A^C)$
• $P(A|B^C) = P(A)$
• $P(A^C|B^C) = P(A^C)$

如果A和B独立，则A的补集和B独立，A和B的补集独立，A的补集和B的补集也独立。即：如果两个事件A和B独立，它们的补集之间的关系也是独立的。