Basic Counting Rules: Union & Product
Combinations and Permutations

基本计数规则 Basic Counting Rules

定义 Definition

并集规则 Union Rule 'or'

并集规则又称“或”规则。如果集合 $S$ 与集合 $T$ 是相交的，那么 $S$ 和 $T$ 的并集 $|S \cup T|$ 的元素个数等于 $|S| + |T|$ 。

乘积规则 Product Rule 'follow by'

乘积规则又称“后”规则。两个集合 $S$ 和 $T$ 的笛卡尔积 $S \times T$ 中的元素个数等于 $|S| · |T|$ 。

计数问题常见策略

直接应用规则：这通常指的是直接使用已知的计数原理或公式来解决问题。
将未知量与已知量关联：比如使用集合的基数（大小）的公式。例子中给出的是两个集合的并和交的基数关系，公式为 $|S| + |T| = |S ∪ T| + |S ∩ T|$ 。这可以帮助我们在知道其中一些集合的大小的情况下，计算其他集合的大小。
找到一个可数集合的双射：双射是一种一一对应的关系，使得每个元素恰好对应一个元素，这可以帮助我们将复杂的计数问题转化为更容易计算的问题。例如，如果我们可以找到一个与已知集合大小相同的集合，并建立双射关系，那么就可以通过计算已知集合的大小来间接计算未知集合的大小。

并集规则 The Union Rule

当前有两个不相交的集合 $S$ 和 $T$ ，有：

|S ∪ T| = |S| + |T|

那么，推广出去，如果有 $n$ 个两两不相交的集合 $S_1, S_2, ... S_n$ ，

|S_1 \cup S_2 ... \cup S_n| = \sum |S_i|

推论

对于任意集合 $X, Y, Z$ ，

|Y \backslash X| = |Y| - |X \cap Y| \\ |X \cup Y| = |X| + |Y| - |X \cap Y| \\ |X \cup Y \cup Z| = |X| + |Y| + |Z| - |X \cap Y| - |Y \cap Z| - |X \cap Z| + |X \cap Y \cap Z|

基本事实

如果两个集合的并集的基数等于两个集合基数的和，那么这两个集合是不相交的。

|S ∪ T| = |S| + |T|

如果多个集合的并集的基数等于这些集合基数的总和，那么这些集合是两两不相交的。

|\bigcup_{i=1}^nS_i| = \sum_{i=1}^n|S_i|

如果一个集合减去另一个集合的结果的基数等于原集合基数减去另一个集合基数的结果，那么第二个集合是第一个集合的子集。

\text{if } |T \backslash S| = |T| - |S| \text{, then } S \subseteq T

乘积规则 The Product Rule

如果要计算多个集合的笛卡尔积的基数，可以将每个集合的基数相乘。

|S₁ × S₂ × ... × Sₖ| = |S₁| · |S₂| · ... · |Sₖ| = \prod_{i=1}^k|S_i|

如果所有的集合 $Sᵢ$ 都等于某个集合 $S$ ，且集合 $S$ 的基数为 $m$ ，那么这些集合的笛卡尔积的基数将是 $m^k$ 。

|S₁ × S₂ × ... × Sₖ| = |S × S × ... × S| = |S|ᵏ = mᵏ

组合对称性 Combinatorial Symmetry

数学对象的对称性是指从对象到其自身的双射映射，这种映射保持了“结构”不变。

（组合）对称性定义了一个等价关系，其中等价类的大小都是相同的。

在计数时，我们通常对“直到对称性”为止的集合感兴趣。也就是说，我们关心的是等价类的数量。

这也可以表述为一种约束，它在每个等价类中识别出一个特定的项（对称约束 Symmectric Constraint）。

k对1函数（k-to-1 function）是一种确切地将k个输入映射到一个输出的函数。
k对1函数定义了组合对称性的等价关系，反之亦然。

组合对称性在解决计数问题时非常有用，特别是在存在可交换性或不可区分性时。通过对称性来分类，可以将问题简化，并只计数唯一的情况而不是所有可能的排列。

例子

给定集合 $Σ = \{a, b, c, d, e\}$ ，问有多少个五字母的单词可以构成，其中字母不重复，且字母a在b前面，在c前面？
从字母集合 $\{a, a, a, d, e\}$ 中，可以构成多少个五字母的单词？

这两个问题的答案将是相同的。

对于第一个问题，因为要求a在b前面且在c前面，所以b和c的相对位置可以是任意的，这使得问题与有多个相同字母a的情况等价，因为a的位置已经预设，所以剩下的d和e的位置也就自由了。两个问题都涉及到了不考虑某些元素的特定顺序的情况，而只计算独特的排列方式。

要解这两个问题，可以用5个位置中选取2个位置来放置d和e，剩下的位置自动由a填充。因此，答案是从5个不同位置中选择2个位置的组合数，即 $C_5^2$ 。

乘积规则在对称性的应用 Product rule: Symmetries and duplications

S₁ 代表考虑了对称性的序列集合。
S₂ 代表对称性本身的集合。
S 代表没有考虑对称性的序列集合。

根据乘积规则，可以把不考虑对称性的序列集合S看作是考虑对称性的序列集合S₁与对称性集合S₂的笛卡尔积。

S = S_1 \times S_2

考虑对称性的序列集合的基数 |S₁| 可以通过将没有考虑对称性的序列集合的基数 |S| 除以对称性集合的基数 |S₂| 来计算。

|S_1| = |S| / |S_2|

换句话说，对称性约束意味着 |S| 序列中的 1/|S₂| 会满足对称性约束。这提供了一种计算在特定对称性约束下序列数量的方法。

组合与排列 Combinations and Permutations

组合对象 Combinatorial Objects

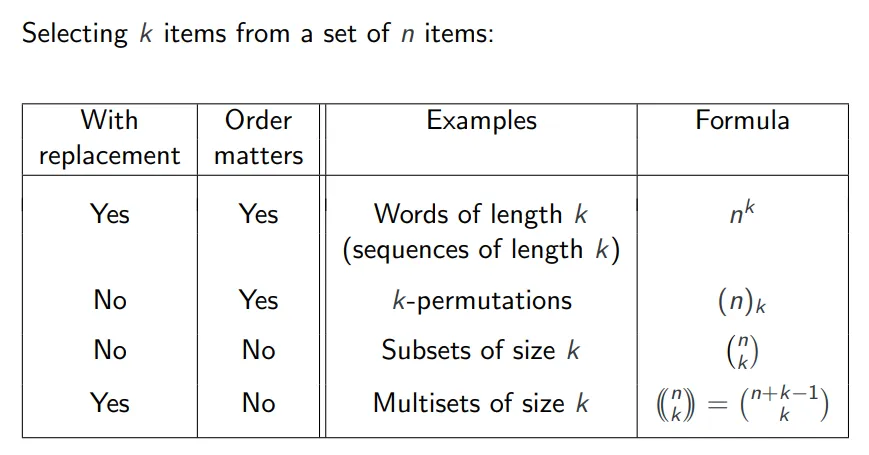
排列（Permutations）：从集合S中选择所有对象的排序，等效于选择所有对象并且认可选择的顺序。

n! = n(n-1)(n-2)...\times 2 \times 1 \\ 0! = 1

r-排列（r-permutations，不重复排列）：：从n个大小的集合S中选择任意r个对象，不重复选择，同时认可选择的顺序。这种选择的数量是 $(n)_r$ ，也表示为 $^nP_r$ 。

^nP_r=n \times (n - 1) ... (n - r + 1) = \frac{n!}{(n-r)!}

n个大小的集合S中选择任意r个不同的对象，不重复选择，同时不考虑选择的顺序。这种选择的数量用组合数表示，即 $C_n^r$ ，或者也可以表示为 $(^n_r)$ ，这就是二项式系数。

(^n_r) = \frac{n!}{r!(n-r)!}

选择物品情景汇总 Selecting items summary

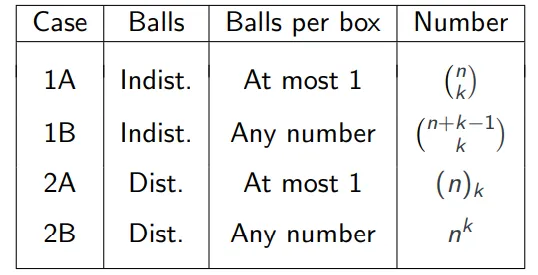
把球放入盒子的问题 Balls in boxes

假设有n个可区分的盒子，有k个球，球可以是：

不可区分的 (Indist.)
可区分的 (Dist.)

问题是：

A. 每个盒子最多放一个球有多少种方法？(At most one)

B. 每个盒子可以放任意数量的球有多少种方法？(Any number of)

对于问题A和B，如果球是不可区分的，情况会有所不同，而如果球是可区分的，每个球可以看作是一个独立的个体。

对于问题A（每个盒子最多一个球），如果球是不可区分的，那么我们就是在计数从集合K到集合N的单射（injective）函数的数量。如果球是可区分的，这相当于计算所有可能的排列，因为我们不能有重复的球在同一个盒子里。

对于问题B（每个盒子可以有任意数量的球），如果球是不可区分的，这通常涉及到将球划分到盒子中，可能使用的是整数划分的方法。如果球是可区分的，那么我们就是在计数从集合K到集合N的所有可能的函数。

目录