COMP9020 Quiz 1,Test started Feb 14, 2024 6:00 PM to Feb 21, 2024 6:00 PM.
Part 1
1.1
Question:
How many integers between -101 and 1001 (inclusive) are divisible by 3?
Answer:
367
本题用 此部分 - 简单理论3 中提到的公式进行计算即可。
⌊31001⌋−⌊3−101−1⌋=333−(−34)=367
1.2
Question
Which of the following will give:
- x+1 if x is an integer, and
- The smallest integer greater than x if x is not an integer.
Select all that apply:
2−⌊1−x⌋
⌈x+1⌉
⌊x⌋+1
2−⌈1−x⌉
⌊x+1⌋
⌈x⌉+1
Answer
⌊x⌋+1
2−⌈1−x⌉
⌊x+1⌋
本题用 此部分 - 简单理论1&2 中提到的公式进行计算即可。
选项1:
2−⌊1−x⌋=2+⌈x−1⌉=⌈x+1⌉
选项2:
选项3:
选项4:
2−⌈1−x⌉=2+⌊x−1⌋=⌊x+1⌋
选项5:
选项6:
1.3
Question
Which of the following is true for all real numbers x?
Select all that apply:
⌈x⌉=⌈⌈x⌉⌉
⌊x⌋<⌈x⌉
⌈⌊x⌋⌉≤⌊⌈x⌉⌋
⌊⌈x⌉⌋≤⌈⌊x⌋⌉
Answer
⌈x⌉=⌈⌈x⌉⌉
⌈⌊x⌋⌉≤⌊⌈x⌉⌋
本题用常理推断即可。
选项1:
由于 ⌈x⌉ 为整数,因此第二层向上取整无效。⌈⌈x⌉⌉=⌈x⌉。
选项2:
∵⌊x⌋≤x, x≤⌈x⌉∴⌊x⌋≤x≤⌈x⌉∴⌊x⌋≤⌈x⌉
- 当 x 为整数时,应当存在等号,因此该选项错误。
选项3:
由于 ⌈x⌉ , ⌊x⌋ 均为整数,因此第二层向上取整和向下取整均无效。
⌈⌊x⌋⌉=⌊x⌋⌊⌈x⌉⌋=⌈x⌉
因此,原不等式变为:
⌊x⌋≤⌈x⌉
选项4:
参考选项3,其可变形为:
⌈x⌉≤⌊x⌋
1.4
Question
Which of the following propositions are true?
Select all that apply:
- For every integer x, there exists an integer y such that x|y.
- For every integer x, there exists an integer y such that y|x.
- There exists an integer y, such that for every integer x, x|y.
- There exists an integer y, such that for every integer x, y|x.
- None of the above
Answer
- For every integer x, there exists an integer y such that y|x.
- There exists an integer y, such that for every integer x, x|y.
本题主要考察 可约分性的定义 。
选项1:
- 当 x=0 时,x∣y 无意义,错误。
选项2:
- 无论 x 的值为多少,都可以使 y=1 ,则: y∣x 成立。正确。
- 1可以整除任何数,包括0。
- 当 x=0 时,仍然成立。即: 1∣0 仍是正确的。
选项3:
- 没有一个整数 y 能做到可以被所有的数字整除。即:x∣y 不可能对任意 x 成立。错误。
选项4:
- 使 y=1 ,则对于任意的 x 均有 y∣x 成立。正确。
- 1可以整除任何数,包括0。
注意
本题需要非常严谨地思考量词与逻辑顺序,这在第一节课是着重强调过的。
- 选项1、选项2,意为:对于任意的值 x,总存在一个与其对应的 y,并使得后面的式子成立。
- 选项3、选项4,意为:存在一个值 y,对于所有的 x 的取值,均能让后面的式子成立。
前两个选项中,对于不同的 x 值, y 的值是可以变化的。而在后两个选项中, y 的值是恒定不变的。
1.5
Question
What is gcd(286,396)?
Answer
22
使用欧里几德算法即可快速算出。略过不表。
2.1
Question
True or False:
For all positive integers m,n and all integers a,b ,
if a=(m)b and a=(n)b ,
then a=(mn)b
Answer
False
因为 m,n不一定是互质的。以下是一个简单的反例:
a=14,b=2m=6,n=4
根据计算可得:
14=(4)214=(6)214=(24)2
2.2
Question
Which of the following will give:
- 1 if x>0
- 0 if x<0
Select all that apply:
- x/(2∣x∣)+1/2
- ∣x+1∣/(2x)
- x−∣x∣
- (x+∣x∣)/(2x)
- x/⌈x⌉
Answer
- x/(2∣x∣)+1/2
- (x+∣x∣)/(2x)
大部分选项错在他们根本没法稳定地仅得到 1 或 0 这两种结果。
选项1:
当 x>0 时,
2∣x∣x+21=21+21=1
当 x<0 时,
2∣x∣x+21=−21+21=0
选项2:
反例:当 x=2时,
2x∣x+1∣=43=1
选项3:
当 x<0 时,
x−∣x∣=x−(−x)=2x=0
选项4:
当 x>0 时,
2xx+∣x∣=2xx+x=1
当 x<0 时,
2xx+∣x∣=2xx−x=0
选项5:
反例:当 x=1.5 时,
⌈x⌉x=⌈1.5⌉1.5=21.5=0.75=1
2.3
Question
Suppose x,y and z are arbitrary integers such that x∣y and y∣z.
Which of the following are always true (i.e. true for any such x,y,z)?
Select all that apply:
- xy∣yz
- xy∣z
- x+y∣z
- x∣yz
- x+y∣y+z
- x∣y+z
Answer
- xy∣yz
- x∣yz
- x∣y+z
依然是关于整除的问题。
已知:
x∣y,y=a∗xy∣z,z=b∗x
因此:
x∣z,z=(a+b)∗x
选项1:
因为 x∣z,即z=k∗x,因此可得:
yz=k∗xy
即:xy∣yz。
选项2:
- 由选项1可知 xy∣yz。当且仅当 y=1 时,xy∣z 。
- 错误。
选项3:
选项4:
已知:
x∣y,y=a∗xy∣z,z=b∗x
故:
yz=abx∗xx∣yz
选项5:
已知:
x∣y,y=a∗xy∣z,z=b∗x
故:
x+y=(a+1)∗xy+z=(a+b)∗xx+yy+z=a+1a+b
- 由于 a+1a+b 不一定为整数,因此不一定有 x+y∣y+z 。错误。
选项6:
已知:
x∣y,y=a∗xy∣z,z=b∗x
故:
y+z=(a+b)∗xxy+z=a+b
2.4
Question
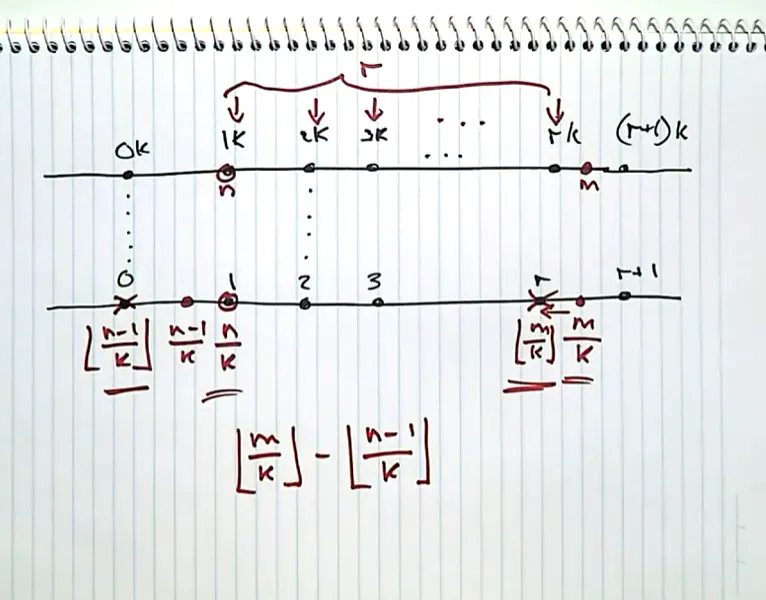
Let m,n and k be arbitrary integers, with k≥1 and n<m.
Which of the following counts the number of multiples of k between n (exclusive) and m (exclusive)?
Select all that apply:
- ⌊(m−1)/k⌋−⌊n/k⌋
- ⌊(m−n−1)/k⌋
- ⌊m/k⌋−⌈n/k⌉
- ⌈m/k⌉−⌊n/k⌋
- ⌊(m−n)/k⌋
Answer
- ⌊(m−1)/k⌋−⌊n/k⌋
其实上课听了倍数数量的证明就知道为什么了,自己画个数轴非常快就明白了。
2.5
Question
Which of the following hold for all real numbers x and y?
Select all that apply:
- ⌊xy⌋≥⌊x⌋⋅⌊y⌋
- ∣xy∣≥∣x∣⋅∣y∣
- ⌊x+y⌋≥⌊x⌋+⌊y⌋
- ∣x+y∣≥∣x∣+∣y∣
- ⌈xy⌉≥⌈x⌉⋅⌈y⌉
- ⌈x+y⌉≥⌈x⌉+⌈y⌉
Answer
- ∣xy∣≥∣x∣⋅∣y∣
- ⌊x+y⌋≥⌊x⌋+⌊y⌋
选项1:
选项2:
其实应该是等号。
选项3:
假设:
x=⌊x⌋+a, a∈[0,1)y=⌊y⌋+b, b∈[0,1)
则有:
x+y=⌊x⌋+⌊y⌋+(a+b)
已知 ⌊x⌋+⌊y⌋ 为整数,那么:
a+b≥1, ⌊x+y⌋>⌊x⌋+⌊y⌋a+b<1, ⌊x+y⌋=⌊x⌋+⌊y⌋
综上所述,⌊x+y⌋≥⌊x⌋+⌊y⌋。
选项4:
当 xy<0 时,会出现 ∣x+y∣<∣x∣+∣y∣。
选项5:
反例:
x=1.1,y=1.1⌈x⌉=2,⌈y⌉=2⌈x⌉⌈y⌉=2∗2=4>⌈xy⌉=⌈1.1∗1.1⌉=⌈1.21⌉=2
选项6:
反例:
x=1.1,y=1.1⌈x⌉=2,⌈y⌉=2⌈x⌉+⌈y⌉=2+2=4>⌈x+y⌉=⌈1.1+1.1⌉=⌈2.2⌉=3
