• Random Variables and Expectations
• Linearity of Expectation
• Expected Time to Success
• Standard Deviation and Variance

随机变量与期望 Random Variables and Expectatiions

随机变量

整数随机变量X是一个从 $Ω$ 到 $ℤ$ 的函数。换句话说，它将每一个结果都与一个数值关联起来。

• 随机变量通常用 X, Y, Z 等字母表示。
• 我们以自然的方式将算术运算扩展到随机变量上。

给定随机变量 $X: Ω → ℤ$ 和随机变量 $Y: Ω → ℤ$ 以及整数 $k$，我们可以将 X、Y 和 k 组合起来，得到以下在所有 $ω ∈ Ω$ 上的函数：

• 变量加法：$X + Y ：ω ↦ X(ω) + Y(ω)$
• 变量乘法：$X · Y ：ω ↦ X(ω) · Y(ω)$
• 标量加法：$X - k ：ω ↦ X(ω) - k$
• 标量乘法：$kX ：ω ↦ k · X(ω)$

期望

随机变量 X 的期望值（通常称为“期望”或“平均值”）是通过下面的公式计算的：

期望是一个真正普遍的概念；它是所有决策、估计盈亏、在风险下行动的基础。在概率论概念出现之前，期望值这一基本概念就已经存在了。

期望值的线性 Linearity of expectation

对于任意随机变量 X 和 Y，以及整数 k，有：

• $E(X+Y) = E(X) + E(Y)$
• $E(k \times X) = k \times E(X)$

观察可得 Observations

如果 $X_1$，$X_2$，...，$X_n$ 是独立同分布的随机变量，那么：

当随机变量独立同分布时，它们和的期望值等于任意一个随机变量期望值的n倍。

尽管 $X_1+X_2+...+X_n$ 与 $nX_1$ 期望值相同，但这两个表达式代表的随机变量本身是非常不同的。

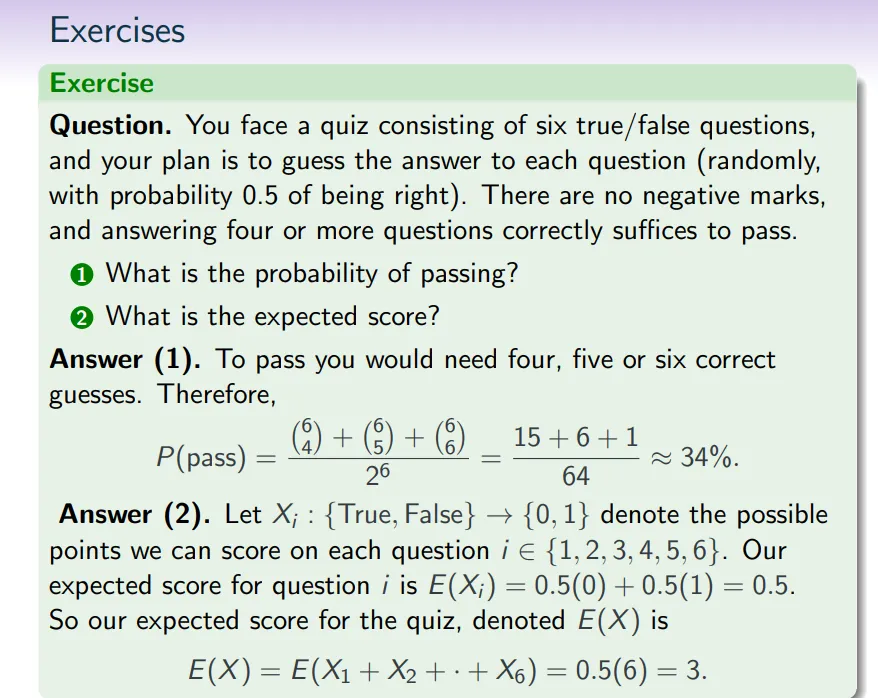
成功的期望时间 Expected Time to Success

几何级数 & 递归

一个更简单但同样有效的论证是，你预期在一次抛掷中得到“一半”的正面，所以你应该期望在两次抛掷中得到一个“完整”的正面。

成功与期望值

问题：高成功概率是否导致高期望值？

一般来说，不是这样。例如：

• 购买更多的彩票可以增加中奖的机会，但是中奖的期望却降低了。

赌徒陷阱 Gambler's ruin

很多所谓的“获胜系统”声称提供一个获胜策略，实际上它们提供了一个频繁获得适度胜利的方案，但代价是偶尔会有非常大的损失。

事实上，有一个正式的定理表明，没有任何系统可以将一个“不公平”的游戏转变为一个“公平”的游戏。在决策理论中，“不公平”指的是那些每个个别投注都有负期望值的游戏。

很容易验证，无论是在轮盘赌上的个别投注，购买彩票，或者任何商业提供的游戏上的投注，都具有负的期望值。

标准差与方差

对于随机变量X，其期望值为 $μ = E(X)$，标准差为：

方差为：

标准差和方差度量了随机变量的值分散程度。方差越小，我们越能确信对于随机选择的 $ω$，有：

并且，方差可以计算为：