目录
- Boolean Logic
- Boolean Functions
- Conjunctive and Disjunctive Normal Form
- Karnaugh Maps
- Boolean Algebras
布尔逻辑
布尔逻辑是关于在一个“简单”的数学结构中进行计算。
- 复杂计算可以完全由这些简单的计算构建
- 可以帮助识别简化措施,这些简化措施可以在电路级别提高性能
- 可以帮助识别简化措施,这些简化措施可以在编程级别提高表现
布尔代数
(两元素)布尔代数被定义为:
集合: B = {0,1}
函数:
- !: B → B
- &&: B² → B
- ||: B² → B
如下所定义:
- !x = (1 - x)
- x && y = min{x, y}
- x || y = max{x, y}

布尔函数 Boolean Function
定义 Definition
一个n元的布尔函数是一个映射:
一个布尔函数只能输出1位的0或1(F/T)。

联结和析取范式 Conjunctive and Disjunctive normal form
- 文字(literal)是一个一元布尔函数。
- 这是最基本的概念。一个文字就是一个变量或者它的否定。比如,x 和 ¬x(或写作 !x)都是文字。
- 最小项(minterm)和最大项(maxterm):
- 最小项是所有变量的AND(与)操作,这些变量可能是原始的,也可能是它们的否定。比如,对于两个变量 x 和 y,x AND ¬y 是一个最小项。
- 最大项是所有变量的OR(或)操作,这些变量可能是原始的,也可能是它们的否定。比如,x OR ¬y 是一个最大项。
- 每个最小项在变量取特定值时只有一个输出为真(1),其他都为假(0);每个最大项在变量取特定值时只有一个输出为假(0),其他都为真(1)。
- 合取范式(CNF, Conjunctive Normal Form):
- 合取范式是一个布尔函数的表示方法,它是由一个或多个最大项组成的AND操作。例如,(x OR y) AND (¬x OR ¬y) 是一个合取范式,因为它是两个最大项 x OR y 和 ¬x OR ¬y 的AND操作。
- 析取范式(DNF, Disjunctive Normal Form):
- 析取范式也是一个布尔函数的表示方法,它是由一个或多个最小项组成的OR操作。例如,(x AND ¬y) OR (¬x AND y) 是一个析取范式,因为它是两个最小项 x AND ¬y 和 ¬x AND y 的OR操作。
简单来说,合取范式像是多个逻辑或表达式的集合,这些表达式被与在一起;析取范式像是多个逻辑与表达式的集合,这些表达式被或在一起。在布尔逻辑中,任何复杂的表达式都可以用这两种范式之一来表示。
注
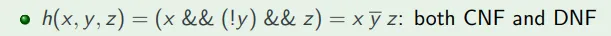
由于 (x && (!y) && z) 本身是AND的集合体(即最小项),所以它可以视为一个仅有一个最小项组成的OR操作的析取范式;
每一个文字,都可以视作仅有一个元素的最小项/最大项,所以(x && (!y) && z)可以看作三个仅有一个元素的最大项的AND操作,即合取范式。
因此,(x && (!y) && z)既是析取范式,又是合取范式。
每一个布尔函数都可以写成DNF和CNF的形式。
标准析取范式 Canonical DNF
定义最小项(Minterm):给定一个n元布尔函数 ,其中 是布尔代数的集合 。对于 中的每个元素 ,定义一个最小项 。这个 是几个 的 AND 运算的结果。每个 要么是变量 ,要么是它的否定 (或 ),这取决于 中对应的元素 。如果 是 1,那么 就是 ;如果 是 0,那么 就是 。
构造DNF公式:对于函数 对每个可能的输入 产生输出 1 的情况,找出所有对应的最小项 。然后,将这些最小项通过 OR 运算(析取)组合起来,形成函数 的析取范式公式 。符号 表示对所有使得 的 对应的最小项 进行 OR 运算。

注
考虑所有可能的输入组合:比如对于两个输入的函数,可能的输入组合有 (0,0), (0,1), (1,0), (1,1)。
找出函数输出为1的所有输入组合:这就是说,我们要找到函数 f 返回1的所有可能情况。
为每个输出为1的情况创建一个最小项:一个最小项是一串用AND连接的输入,如果输入是1我们就直接写下它,如果是0我们就写它的否定形式(比如 !x 或 ¬x)。例如,如果 x=1, y=0 时函数输出为1,那么对应的最小项就是 x AND !y。
将所有这些最小项用OR连接起来:这样做就创建了一个表达式,它精确地描述了函数 f 何时会输出1。如果我们有多个最小项,我们就把它们用OR(||)连接起来,表示这个函数在这些最小项对应的输入情况下都会输出1。

卡诺图 Karnaugh Maps
制作卡诺图: 根据你的变量个数,画出一个表格。比如两个变量就画2x2的表格,三个变量就画2x4的表格,四个变量则是4x4的表格。
标记变量:表格的行和列要代表所有变量可能的状态组合,这些状态要按格雷码顺序排列,也就是说,每次只变化一个变量的状态。(例:00 - 01 - 11 - 10)
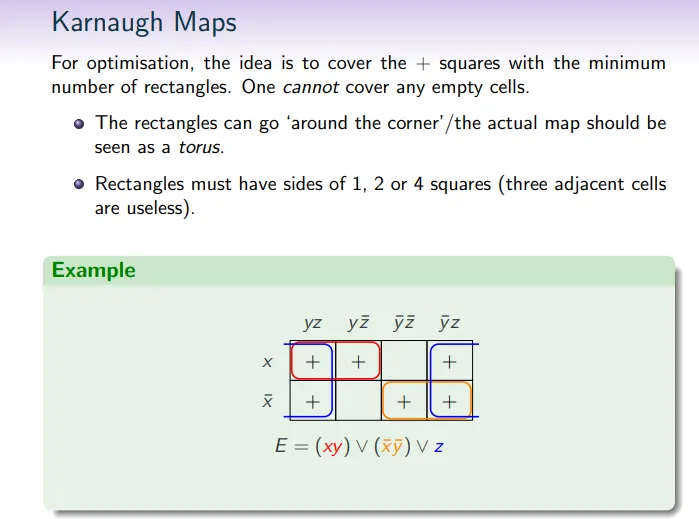
找规律:找出那些可以合并的标记的格子。合并的原则是形成尽可能大的矩形区域,且每个矩形里的单元格数必须是2的幂次个(1, 2, 4...)。这些矩形代表了函数的简化形式。
写出表达式:每一个矩形都对应一个表达式的部分,你只需查看未改变的变量,将它们连接起来。如果变量在矩形中的所有单元格中都是1,就直接写这个变量;如果都是0,就写它的否定形式。如果变量在矩形内的状态既有0也有1,就忽略这个变量。
合并表达式:最后,将所有找到的矩形对应的表达式用OR连接起来,这就是简化后的布尔表达式。

布尔代数 Boolean Algebra
性质
交换律(Commutativity):
结合律(Associativity):
分配律(Distributivity):
同一律(Identity):
补足律(Complementation):




对偶性 Duality
对偶性定义: 如果 是用变量(比如 )和常数(0 和 1)以及布尔代数操作(∧ 表示与,∨ 表示或,′ 表示非)定义的表达式,那么 的对偶表达式 就是通过将所有的 ∧ 替换为 ∨,将所有的 ∨ 替换为 ∧,将所有的 0 替换为 1,将所有的 1 替换为 0 得到的。
布尔代数的对偶: 如果有一个布尔代数 ,它的对偶布尔代数是 。这里只是交换了与(∧)和或(∨)操作,以及常数 0 和 1 的位置。
对偶性原理定理: 如果你能通过布尔代数的定律证明 ,那么 也成立。这个原理告诉我们,一个布尔等式的对偶等式也是成立的。
本文作者:Jeff Wu
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!