COMP9020 Quiz 3

QUIZ 3

1.1

Question

Consider the graph with:

vertex set {0,1}×{0,1}×{0,1}
an edge between two vertices if they differ in exactly two co-ordinates

What is the degree sequence of this graph?

Select one alternative:


- 1,1,1,1,1,1,1,1
- 0,0,2,2,2,2,0,0
- 0,4,4,0,0,00,0,0
- 0,0,0,8,0,0,0,0
- None of the above

Answer

首先这是一个无向图。

其次，这个顶点集的坐标是一个三阶向量，每一位都由0或1组成。因此，顶点有如下几种：


(0,0,0) (0,0,1) (0,1,0) (0,1,1)
(1,0,0) (1,0,1) (1,1,0) (1,1,1)

现在，对相互之间位数差异位2的点互相连线以构成边，所以只需要考虑哪些点跟其相差有2即可。

但换句话说，这也可以考虑保留一位，另外两位都不同即可。而每一个坐标一共有三位，所以每个点都可以与另外三个点进行连线，换句话说每个点都有三个度。

因此，答案为：


3,3,3,3,3,3,3,3

None of the above

1.2

Question

Which of the following graphs are isomorphic to this graph:

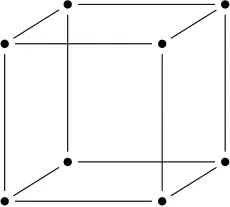
Select all that apply:

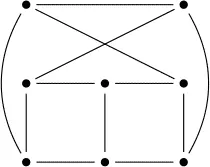
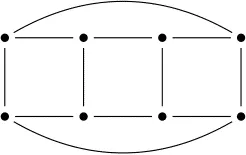
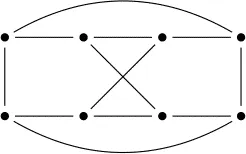
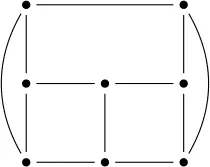
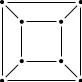
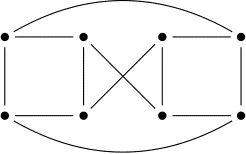
Answer

画图，设点，一点点推，找到矛盾边、矛盾点即可排除。

答案为：

1.3

Question

Starting from Vertex 0, which of the following sequences of vertices could arise as a sequence of explored vertices when performing a breadth-first traversal (according to lectures)?

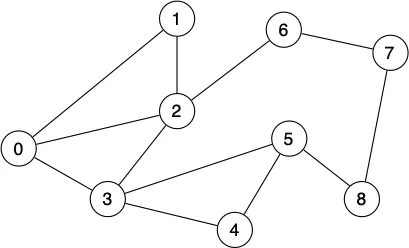
Select all that apply:


- 0,2,1,3,5,4,8,6,7
- 0,1,2,3,6,5,4,7,8
- 0,3,2,1,4,5,6,8,7
- 0,3,5,8,7,6,4,2,1
- 0,1,3,4,5,8,7,6,2
- 0,1,2,3,4,5,6,7,8

Answer

该图像的同构如图所示：

则根据广度优先算法，我们应当为每一层先进行遍历，再进行下一层。

答案为：


- 0,1,2,3,6,5,4,7,8
- 0,3,2,1,4,5,6,8,7
- 0,1,2,3,4,5,6,7,8

1.4

Question

Starting from Vertex 0, which of the following sequences of vertices could arise as a sequence of explored vertices when performing a depth-first traversal (according to lectures)?

Select all that apply:


- 0,1,3,4,5,8,7,6,2
- 0,3,2,1,4,5,6,8,7
- 0,2,1,3,5,4,8,6,7
- 0,3,5,8,7,6,4,2,1
- 0,1,2,3,6,5,4,7,8
- 0,1,2,3,4,5,6,7,8

Answer

可以自己画图试验一下，一个一个试即可。注意：需要给每一个还未遍历但已经被父节点发现的点标注深度，并且一个点不能被重复标注深度。

答案为：


- 0,1,3,4,5,8,7,6,2
- 0,3,5,8,7,6,4,2,1

1.5

Question

Which of the following properties does this graph have?

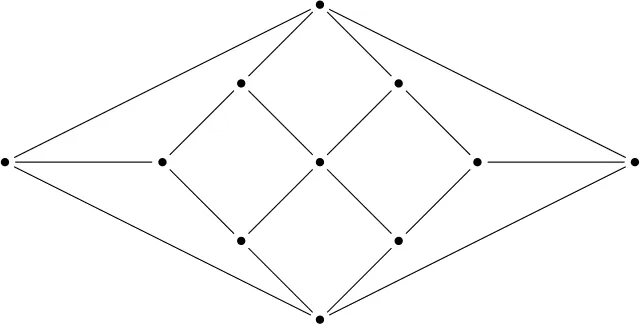
Select all that apply:


- Contains a cycle of length 10
- Bipartite
- Planar
- Hamiltonian path
- Connected
- Chromatic number 3
- Clique number 2
- Eulerian path

Answer

首先为图中的每个点标注序号，方便进行表示。

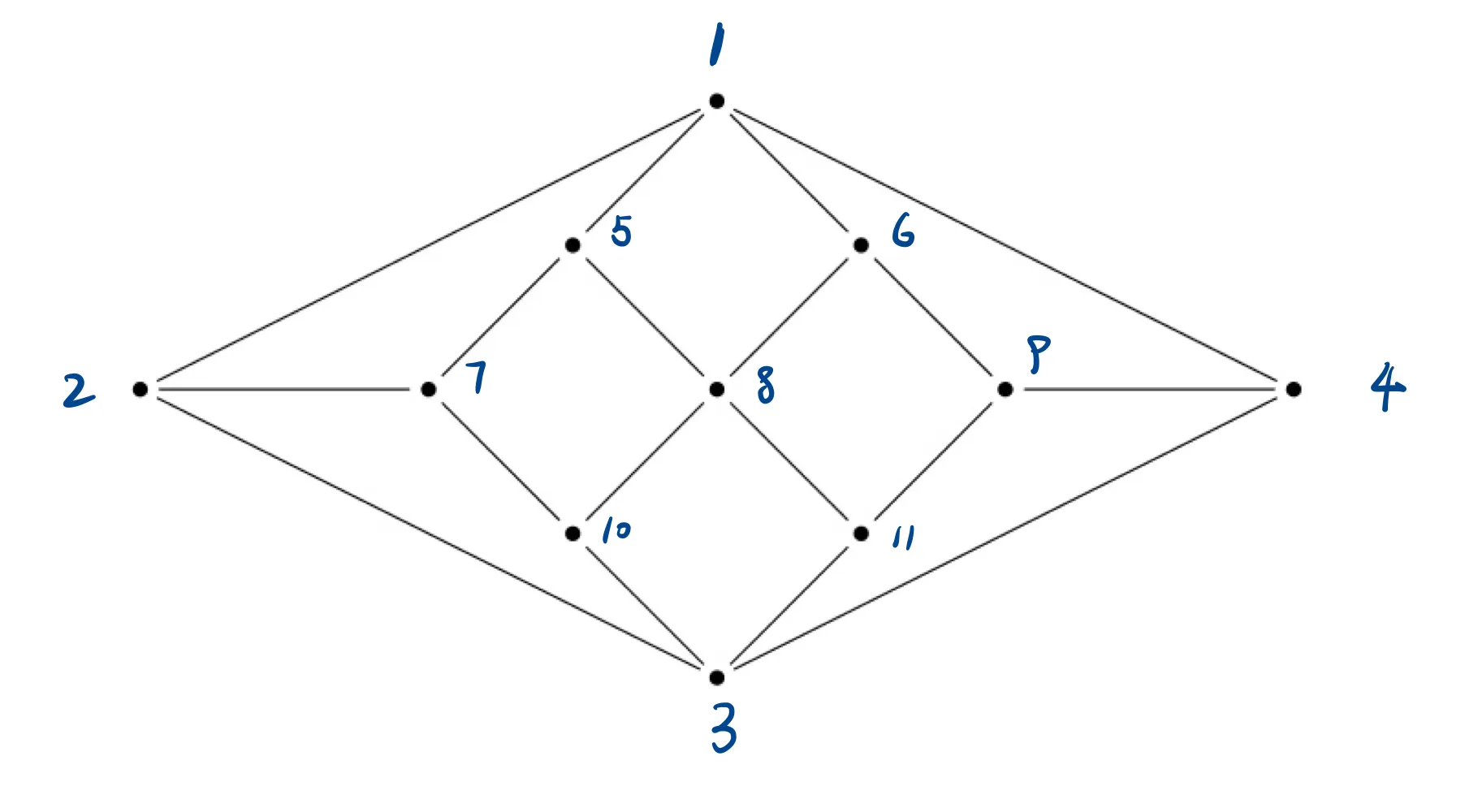
选项1：循环路径如下。

1 \to 2 \to 3 \to 10 \to 7 \to 5 \to 8 \to 11 \to 9 \to 4 \to 1

选项2：通过染色法可尝试证明。如果图能被着成二色，说明是二分的。

black: [1] \\ white: [2, 4, 5, 6] \\ black: [3, 7, 8, 9] \\ white: [10, 11] \\

选项3：显然它没有任何的边有相交，因此它是平面的。
选项4：不存在，难以证明，但确实不存在。
选项5：正确的，每一对顶点都存在路径到达。
选项6：上文以证明，色数为2。
选项7：由于色数大于等于团数，因此团数最大为2。而找到一条边即包含两个顶点，因此团数可以为2。
选项8：对于连通图来说，存在欧拉路径的条件式每个点的度数为偶数或恰好两个顶点的度数是奇数。显然，2, 4, 5, 6, 7, 9, 10, 11的度数都为基数，因此不存在欧拉路径。

因此，答案为：


- Contains a cycle of length 10
- Bipartite
- Planar
- Connected
- Clique number 2

2.1

Question

Which of the following statements are true for any graph with n≥1 vertices and m≥0 edges?

Select all that apply:


- If m < n then the graph is acyclic
- If m ≥ n-1 then the graph is connected
- If m ≥ n then the graph contains a cycle
- If m < n-1 then the graph is not connected

Answer

选项1：错误。例如，当前有一个点离散在外，另外n-1个点首尾相接，满足m=n-1<n，然而该图具有环。
选项2：错误。例如，当前有一个点离散在外，另外n-1个点首尾相接，满足m=n-1，然而该图并不连通。
选项3：正确。在一个有 n 个顶点的图中，如果有至少 n 条边，那么至少有一个顶点的度数大于 1，这意味着在这些顶点中形成了一个环。因为一棵树（没有环的连通图）恰好有 n-1 条边，所以任何边数超过 n-1 的图至少有一个环。
选项4：正确。一个有 n 个顶点的图要形成连通图，至少需要 n-1 条边来形成一棵树（树是最少边数的连通图）。如果边的数目少于 n-1，那么一定存在至少一个顶点与图的其他部分不连通。

因此，答案为：


- If m ≥ n then the graph contains a cycle
- If m < n-1 then the graph is not connected

2.2

Question

Let D0, D1, D2, D3 be the degree sequence of a tree with n≥2 vertices (assume Dk = 0 for k≥4)

Which of the following must necessarily hold:

Select all that apply


- D1 is even
- D3 ≥ D2
- D2 ≥ D3
- D1 = 2 + D3
- D0 = 0
- D1 ≥ 2

Answer

对于一棵有 n 个顶点的树，以下性质始终成立：

它有 n-1 条边。
至少有两个顶点的度数是 1（也就是说，至少有两个叶子节点）。
树中没有度数为 0 的顶点，因为树是连通的。

由于在大于等于4的情况下，Dk=0，我们可以认为没有度数大于等于4的节点。

选项1：错误。至少有两个顶点度数是1，但不一定意味着一直都是偶数。反例如下，D1=3
```
 o  o  o
 |  |  |
 o  o  o
  \ | /
    o
```
选项2：错误。反例如下，D3=1，D2=3
```
 o  o  o
 |  |  |
 o  o  o
  \ | /
    o
```
选项3：错误。反例如下，D3=1，D2=0
```
 o  o  o
  \ | /
    o
```
选项4：正确。设一棵树T有n个顶点，那么它有n-1条边，度数总数则为2(n-1) = 2n-4。由于树没有环，所以每增加一个度数为3的顶点，必须至少增加两个度数为1的顶点（叶子节点）来保持树的结构。这是因为度数为3的顶点在不增加环的情况下提供了两个额外的边缘连接点，这些连接点必须由叶子节点来平衡，因为叶子节点只会增加一个连接点。
选项5：正确。树是连通的，因此不存在度数为0的点。
选项6：正确。树中至少有两个叶子结点。

因此，答案为：


- D1 = 2 + D3
- D0 = 0
- D1 ≥ 2

2.3

Question

Which of the following graphs have an Eulerian circuit?

Select all that apply

$K_{5,5}$
All graphs with degree sequence 0,0,5,0,5
All regular graphs with 5 vertices and 10 edges
All graphs with degree sequence 0,0,3,0,3,0,3
$K_5$
$K_{5,5,5}$

Answer

存在欧拉回路的条件：

所有的点的度数都为偶数。
不满足1，那么需要恰好有两个点的度数为奇数。

选项1：错误。由于每一个点都和另外集合内所有点有对应关系，因此所有的点的度数都为5。
选项2：错误。不连通。
选项3：正确。由于10 = 5*(5-1)，所以这个图是一个完全图。每一个点的度数均为5-1=4。
选项4：错误。不连通。
选项5：正确。这个图是一个完全图。每一个点的度数均为5-1=4。
选项6：正确。这个图是一个完全三部图，每一个点的度数为5+5=10。

因此，答案为：


- All regular graphs with 5 vertices and 10 edges
- K_5
- K_{5,5,5}

2.4

Question

Let G be a finite directed graph where every vertex has in-degree and out-degree at most 1.

True or false:

G has a vertex of out-degree 0 if and only if G has a vertex of in-degree 0.

Answer

在一个有限的有向图G中，如果每个顶点的入度和出度最多为1，这意味着每个顶点要么与一个其他顶点相连（作为其唯一的前驱或后继），要么完全不与任何顶点相连（入度和出度都为0）。

为了理解为什么这个陈述是真的，我们可以考虑以下情况：

如果G有一个出度为0的顶点，那么这意味着有一个顶点没有指向任何其他顶点的边。由于图是有限的，并且每个顶点的连接数是受限的（最多1个出度和1个入度），这意味着必须有至少一个顶点的入度为0，因为否则会形成一个封闭的环，使得每个顶点都有出度和入度，这与假设矛盾。

反过来，如果G有一个入度为0的顶点，这意味着有一个顶点没有任何从其他顶点指向它的边。考虑到图中顶点数量有限，以及每个顶点的连接数受限，这就意味着必须有至少一个顶点的出度为0，以防止形成一个完全封闭的环路。否则，如果每个顶点都有一个出度，那么每个顶点也必须有一个入度，以保持平衡，这会导致每个顶点既是某个环的一部分，又是该环的出发点，这与入度为0的假设矛盾。

因此，这个陈述展示了在这种类型的图中，出度为0的顶点的存在必然意味着有一个入度为0的顶点的存在，反之亦然。这是由于图的有限性和每个顶点入度及出度的限制共同决定的。

因此，答案为：


True

2.5

Question

True or false:

If a graph has chromatic number at least 3, then it must contain a subdivision of K3

Answer

显然错误。一个环图如果有奇数个点，那么它的色数必然等于3，然而一个环图并不一定是 $K_3$ 。

因此，答案为：


False

目录

1.1

Question

Answer

1.2

Question

Answer

1.3

Question

Answer

1.4

Question

Answer

1.5

Question

Answer

2.1

Question

Answer

2.2

Question

Answer

2.3

Question

Answer

2.4

Question

Answer

2.5

Question

Answer