目录
Lecture 5: Graph Theory
- Terminology and Notation
- Graph Traversals
- Properties of Graphs
符号与术语 Terminology and Notation
图 Graph
集合对代表图:
- - 所有的顶点的集合(vertices)
- - 所有的边的集合(edges)
无向图 Undirected Graph
在无向图中,每条边事一个包含两个顶点的集合,即边可以表示为,其中是顶点集中的元素,并且有。
有向图 Directed Graph
在有向图中,每条边(也称作弧 arc)是一个有序的顶点对,即边可以表示为,其中是顶点集中的元素,并且可以有。
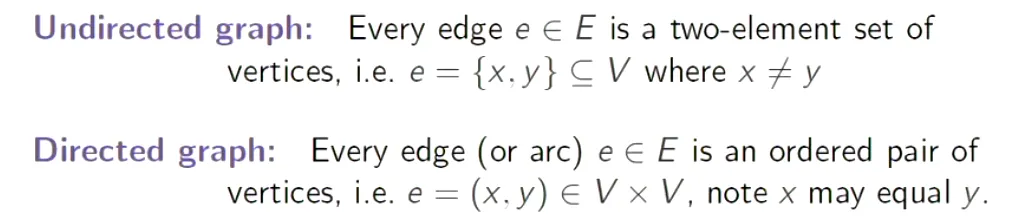
邻接矩阵 Adjacency Matrix
将每一个点同时作为矩阵的行与列,并将边的起点和终点对应的点的坐标置为1。
注意:有向图中,需要严格规定行/列为起点和终点。无向图中,由于互为起点/终点,所以必为对称矩阵,不需要严格规定行/列为起点或终点。

邻接表 Adjacency List
将每一个点都列出来,并将以此点为起点的边所对应的终点都列出来。
注意:无向图中,应当将所有与该点相连的点都列出来。

关联矩阵 Incidence Matrix
以点为行,以所有的边为列。
在无向图中,如果点包含在此边中,则将值置为1,否则置为0。
在有向图中,如果点包含在此边中且为起点,则将值置为-1,如果为终点,置为1,否则置为0。

路径 Path
路径有很多概念。这里说的路径是一种广义的叫法。
(有向)游走 (directed) walk
是顶点和边的序列,这些边依次连接序列中的顶点。
即,如果有序列:
就有游走:
我们可以如此表示:
迹 trail
是一种特殊的游走。在迹中,不存在重复的边。
路径 path
是一种特殊的游走。在路径中,不存在重复的顶点。
路径长度 length
是路径中行走过的边的数量,一般记为 。
注意:路径的边和顶点都不能使重复的。
子路径/子游走 subpath/subwalk
指路径/游走的一部分,长度一般表示为 。
长度为0的路径 path of length 0
指单个顶点 。
连通
连通集/图(无向图) connected set / graph
如果无向图中每一对顶点都至少存在一条路径,那么称该图为连通图。
强连通集/图(有向图) strongly connected set / graph
如果有向图中每一对不同顶点 和 之间都存在从 到 和从 到 的有向路径,那么称该图为强连通图。
连通分量 connected component
给定一个无向图 ,连通分量遵循如下定义:
- 连通分量是 的一个最大顶点子集 ,在 中,任意两个顶点都是可以连通的。
- 连通分量是最大顶点子集,意味着如果尝试添加任何新的外部顶点,新顶点一定不能通过已有的边和所有的其他顶点保持连通性。
顶点度数 Vertex Degrees
无向图顶点度数性质
在无向图中,顶点度数是与该顶点相连的边的数量:
该定义意为:在图 中所有和点 直接以边相连的点 的集合的基数。
值得注意的是,对于一般的无向图,所有顶点的度数之和等于边的数量的2倍,原因在于一个边会被两头的点各算一次度数。
由此还可以得出另一个引理:在无向图中,具有奇数度数的顶点数量一定是偶数。
有向图顶点度数性质
在有向图中,有两种度数概念:出度(out-degree)和入度(in-degree)。
- 出度(out-degree):表示有多少条边从该顶点出发指向其他顶点。点 的出度是图中以该点为起点的边的数量。
- 入度(in-degree):表示有多少条边指向该顶点。点 的入度是图中以该点为终点的边的数量。
值得注意的是,对于一般的无向图,所有顶点的入度之和等于所有顶点的出度之和,同时等于边的数量,原因在于一个边刚好会被出度和入度各计算一次。
循环 cycles
现在有一条游走:
- 封闭游走(closed walk):起点 = 终点 。
- 循环(cycle):首先是一种封闭游走,其次在有向图中长度至少为2,无向图中长度至少为3,经过的顶点除了起点和终点之外各不相同。
- 无循环游走(acyclic walk):等同于路径。所有的顶点都不相同。
所有顶点不相同的意思即不会多次经过相同的点。
循环特性
如果 是一个循环,那么移除任何一条边都会留下一个路径。这个性质表明循环不依赖于任何单一的边,而是由多条边形成的闭合的链。
循环的定义
如果一个游走有与顶点数相同数量的边,并且没有任何真子游走(即除了游走本身以外的部分)具有这个性质,则这个游走是一个循环。
这个条件表明,如果一个图 的边数 等于定点数 ,并且图不包含任何的循环,那么图 本身就是一个循环。如果图包含于顶点数量相同数量的边,但是它不是一个循环,那么它必定包含至少一个循环。
树 tree
定义
- 无环图(Acyclic Graph):一个不包含任何循环的图。
- 树(Tree):一个连通的无环无向图。
- 森林(Forest):由多棵不相交的树组成的图。即:每个连通分量都是一棵树的图。
性质
- 一个图 是树的充分必要条件是它是无环的并且满足 。这意味着图中顶点的数量比边的数量多一个。这也隐含了图是连通的,因为如果图不连通,那么至少会有一个顶点不能通过边与其他顶点相连,这会使得 。
- 在一棵树中,任意两个顶点之间都有且只有一条唯一的路径相连。如果存在多于一条路径,则必然会形成循环,这与树的无环性质相矛盾。
- 如果移除树中的任何一条边,图会变得不连通,因为那条边是连接两个顶点唯一的路径的一部分。
- 如果在树中添加任何一条新边连接任意两个已存在的顶点,将会形成一个循环,因为在原本的树中这两个顶点已经通过唯一的路径相连。添加的边会提供一个额外的路径,从而创建一个循环。
有根树 rotted tree
是一棵树,其中有一个特定的顶点被指定为根(Root)。在有根树中,边有明确的方向,即从根指向外部的方向,从父节点指向子节点。
在有根树中,每个节点都有一个层级数(Level Number)或深度(Depth),这表示该节点从根节点到该节点的最短路径上的边的数量。
另一个在计算机科学中常见的概念是有向无环图(Directed Acyclic Graph, DAG),这是一种图,其中的边具有方向,并且图中没有任何循环。每个有向无环图的顶点都可以进行拓扑排序,即可以把所有的顶点排列成一个线性序列,使得对于图中的每一条有向边 ,顶点 都在顶点 之前。
特殊的图 special graphs
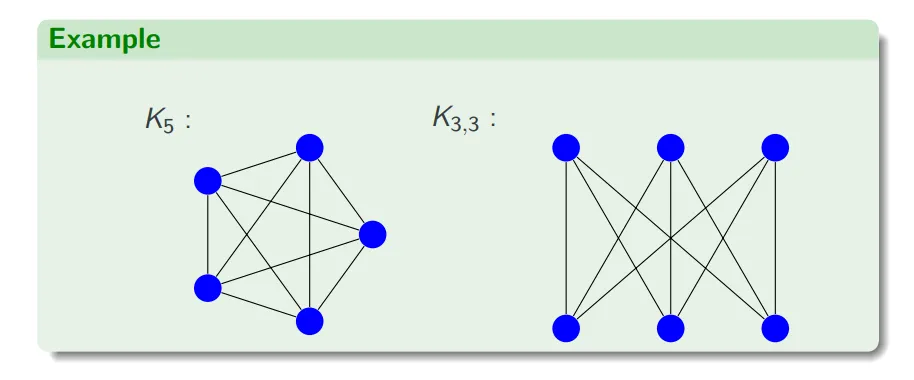
完全图 complete graph
一般记作 。
有n个顶点,有 条边。
即:每对顶点之间都恰好有一条边相连。
完全二部图 complete bipartite graph
一般记作 。
包含 个顶点,这些顶点被分为两个不相交的集合,一个包含 个顶点,一个包含 个顶点。每个集合内部的顶点之间没有边相连,但是集合之间的每对顶点都有一条边相连。
即:完全二部图的边数是 。
完全k部图 complete k-partite graph
一般记作 。
包含 个顶点,被分为不相交的k个集合,其余定义可参考完全二部图。
因为每个集合中的顶点都与其他集合中的所有顶点相连,完全k部图的边数如下:

图的同构 graph isomorphisms
图的同构(Graph Isomorphisms)是图论中的一个基本概念,它描述了两个图在结构上是否是完全等价关系。
两个图是同构的,就意味着它们本质上是相同的图,只是顶点的标记或者布局可能不同。可以通过重新标记顶点的方式,从一个图得到另一个图。同构的两个图有相同数量的顶点连接相同数量的边,顶点之间的连通方式也是一致的。
双射
双射是一种特殊的函数,它同时满足以下两个条件:
- 单射(Injective):函数的每一个元素映射到不同的元素,即没有两个不同的元素映射到同一个元素。
- 满射(Surjective):函数的映射涵盖了所有可能的元素,即每个元素至少被映射到一次。
当一个函数既是单射又是满射时,它就是双射。在图同构中,双射意味着图 G 的每个顶点都精确对应到图 H 的一个独特顶点,没有遗漏也没有重复。
映射 被称为图的同构,需要满足以下条件:
- 是一个从图 的顶点集 到图 的顶点集 的双射。【点的对应关系】
- 对于图 中任意两个顶点 和 ,如果边 存在于图 的边集 中,当且仅当边 存在于图 的边集 中。即:如果图 中两个顶点相连,那么在图 中 它们对应的顶点也相连,反之亦然。【边的对应关系】
如果存在至少一个这样的同构 ,则称两个图 和 是同构的(Isomorphic)。同构关系说明了尽管两个图在顶点的标记或绘制方式上可能不同,它们的结构是一样的。我们可以通过重新标记和重新连接边的方式,将一个图变换成另一个图。
在实际应用中,判断两个图是否同构通常是一个困难的问题,目前还没有已知的多项式时间算法能够解决这个问题,它是图论和理论计算机科学中的一个著名问题。
图的遍历
定义
图的探索通常涉及按某种顺序访问图的所有顶点。探索图的过程分为两类:
-
搜索(Search):这是探索图的过程,直到找到一个特定的顶点。这个过程可能在找到目标顶点之前不会遍历图中的所有顶点。搜索的常见算法包括深度优先搜索(DFS)和广度优先搜索(BFS),它们在找到所需顶点后可以停止。
-
遍历(Traversal):在这个过程中,会检查图中的每一个顶点,确保每个顶点都被访问过。遍历的目的是对图进行全面的检查,而不仅仅是找到一个顶点。深度优先遍历和广度优先遍历是两种常用的遍历方法,它们都可以确保访问图中的每一个顶点。遍历可以用来绘制图、检测图中的循环、找到图中的连通分量等。
两种常用方法
- 深度优先搜索/遍历(depth-first search/traversal)(DFS)
- 广度优先搜索/遍历(breadth-first search/traversal)(BFS)
尽管这两种算法在探索过程中采用的策略不同,但它们都遵循以下基本结构:
- 检查顶点:选择一个顶点 进行检查。
- 发现新顶点:查找顶点 的所有邻居。
- 移动到下一个顶点:选择下一个已经发现但尚未检查的顶点,然后对其执行上述步骤。
对于深度优先搜索(DFS),算法尝试沿着图的一条路径尽可能深地进行,直到该路径的末端,然后回溯到前一个顶点,以探索未检查的路径。这通常使用递归或者栈来实现。
对于广度优先搜索(BFS),算法首先检查起始顶点的所有直接邻居,然后再对这些邻居的邻居进行检查,以此类推。这种方式使得探索可以按照距离起点的层数(层级)来进行,通常使用队列来实现。
深度优先搜索通常用于寻找路径或检查图中是否存在循环,而广度优先搜索常用于找到最短路径或检查图的连通性。
特殊的遍历方式 special types of traversals
在图探索中,存在一些具有特殊性质的遍历方式:
-
欧拉遍历(Eulerian Traversal):在这种遍历中,一个人会访问图中的每一条边恰好一次,并且遍历可以结束在开始的顶点或者在不同的顶点。如果它结束在开始的顶点,这样的遍历称为欧拉回路或欧拉环路。
-
哈密顿遍历(Hamiltonian Traversal):在哈密顿遍历中,一个人会访问图中的每一个顶点恰好一次,并且遍历可以结束在开始的顶点或者在不同的顶点。如果它结束在开始的顶点,这样的遍历称为哈密顿回路。
对于给定的图,欧拉遍历或哈密顿遍历可能存在也可能不存在。识别图是否具有这些遍历的问题(即决策问题)和找到这样的遍历的过程(即搜索问题)是两个微妙而不同的问题。
- 决策问题涉及确定图中是否存在这样的遍历。
- 搜索问题则是在已知这样的遍历存在的情况下找到它。
对于欧拉遍历,存在已知的多项式时间复杂度的算法来确定其存在性和找到该遍历。而对于哈密顿遍历,确定图是否有哈密顿路径或回路是一个已知的NP-完全问题,这意味着目前没有已知的多项式时间算法可以解决所有情况。
边的遍历 edge traversal
对于一个图 来说,
- 欧拉路径(Euler Trail):在途中每条边恰好被访问一次的路径。
- 欧拉回路(Euler Circuit):起点和终点完全相同,形成闭合循环的欧拉路径。
对于连通图 来说,包含欧拉回路的条件为:
- 每一个顶点的度数都是偶数。
对于连通图 来说,包含一个欧拉路径(不一定是回路)的条件为:
- 要么图包含一个欧拉回路(在这种情况下每个顶点的度数都是偶数);
- 要么图有恰好两个顶点的度数是奇数(这两个顶点是欧拉路径的起点和终点)。
对于有向图,一个图存在欧拉回路的条件稍有不同:
- 每个顶点的入度和出度相同。
顶点的遍历 vertex traversal
对于一个图 来说,
- 哈密顿路径(Hamiltonian Path):是一条遍历图的路径,它访问每个顶点恰好一次。
- 哈密顿回路(Hamiltonian Cycle):是一个哈密顿路径,它返回到起始顶点,形成一个闭环,并且除了起始顶点不重复访问任何顶点。
找到一个哈密顿回路,或者证明它不存在,在计算上是一个困难的问题。最坏情况下,这个问题是NP完全的,意味着没有已知的多项式时间算法可以解决所有实例。
一些有哈密顿回路存在的例子
- 所有五种正多面体都有哈密顿回路。
- n-立方体有一个哈密顿回路,这个是使用格雷码(Gray Code)构造的。
- 完全图 对所有的 都有哈密顿回路。
- 完全二部图 存在哈密顿回路,当且仅当 。
- 如果三个数 满足三角不等式,那么完全三部图 也有哈密顿回路。三角不等式意为:
- 骑士在国际象棋棋盘上的巡游问题也涉及哈密顿回路的构造,包括在矩形棋盘上。
当我们试图构造一个不存在哈密顿回路的图时,任务很可能变得复杂。这是因为找到一个哈密顿回路不存在的例子通常需要考虑和检验多种可能的路径组合。
对于给定的图,验证是否存在哈密顿回路不是一件显而易见的事情。没有一种简单的方法可以立即告诉我们图是否具有这个性质,除非我们检查所有可能的顶点排列组合。这使得证明一个图不包含哈密顿回路成为一个非常复杂的问题。
然而,相比之下,如果已经给出了一个特定的回路,验证这个回路是否是哈密顿回路则是简单的。我们只需要检查这个回路是否经过了图中的每一个顶点恰好一次,并且起点和终点是同一个顶点。
图的性质 properties of graphs
图的着色 colouring
定义
非正式定义:给图中的每个顶点分配一个颜色,使得任何两个通过一条边相连的顶点都拥有不同的颜色。
正式定义:一个映射 ,使得对图中的每一条边 ,顶点 和 的颜色都不相同,即 。
色数 chromatic number
实现上述颜色分配所需要的最小颜色数 ,记作 。
色数在运筹学中非常重要,尤其是在调度问题中。例如,在考试调度中,每个考试是一个顶点,考试之间的冲突(如同一组学生需要参加的两场考试)由边表示,目标是将考试安排在尽可能少的时间段内进行,同时确保没有学生需要在同一时间参加两场考试。
此外,还有一个与顶点着色相对的概念是边着色,边着色要求图中共享一个顶点的任意两条边都有不同的颜色。尽管边着色在理论上很有趣,但在实践中它不如顶点着色常用。
色数的性质 properties of the chromatic number
- 对于完全图 而言, 。
- 如果图 有 个顶点,且 ,则该图为完全图 。
TIPS
假设相比于完全图 ,图 缺少了边 ,那么在着色时,我们需要将点 去除,为其他的点着 种颜色,最后将点 着与点 完全相同的颜色即可。
- 如果 ,那么可以说图是完全分离的,即图不存在边。
- 如果 ,那么可以说图是二分的。
- 对于任何树 来说,。
- 对于任何环形图 来说,它的色数取决于点数 的奇偶性。
- 如果n是偶数,那么:
- 如果n是奇数,那么:
团 cliques
在图论中,团(clique)是一个图的子图,满足子图中任意两个顶点都相互连接。也就是说,在这个子图中,每一对顶点之间都有边相连。这样的子图被称为“完全子图”,因为它的连通性是完整的,没有缺少任何可能的边。
在无向图 中,若 是顶点集 的一个子集,并且对于它之中的每一对不同的顶点 和 ,都有边 ,那么图 是图 的一个完全子图,其中 是边集 中所有连接 中顶点的边的集合。如果 是 的一个完全子图,那么 就是 的一个团。
注
在第一段中,团被定义为一个子图;在第二段中,团被定义为一个点的集合。事实上,它在不同的上下文中可能会具有不同的概念。
严格来说,团是指一组顶点。
如果一个团包含k个节点,那么它被称为k-团。最大团的大小被称为图的团数,记作 。
图的色数和图的团数有如下关系:
因为一个团中的每个顶点都需要一个不同的颜色,因此至少需要 种颜色。
实际上,对于任意给定的团数k,总是可以构造一个图,使得它的色数远大于k。这就意味着,尽管团数提供了一个色数的下界,但图的实际色数可能会比这个下界大得多,而且理论上可以无限大。
团的性质
- :在一个完全图中,每个顶点都与其他所有顶点相连,因此最大团的大小等于顶点的数量,即n。
- :在一个二分图(由两个顶点集构成,每个集合内的顶点之间没有边相连)中,最大团大小为2,因为你只能在两个顶点集中各取一个顶点来形成一个团。
- :在一个完全r部图中(顶点被分成r个互不相连的集合),最大团的大小是r。因为最大的团可以从每个集合中取一个顶点来形成。
- 如果 ,说明图中没有边。
- 对于所有树 ,均有 :因为树中没有环,最大团的大小只能是2(任何两个相连的顶点都可以形成一个团)。
- 对于环形图 来说,
- 因为环中任意相邻的两个顶点都可以形成一个团,但不可能有三个互相连接的顶点形成更大的团。
注
有些图的团数是2,但不一定意味着这个图是二分图。
例如,对于任何奇数 构成的环形图 ,即使团数是2,色数 。这是因为在一个奇数个顶点的环中,至少需要三种颜色才能保证相邻顶点颜色不同。
时间表调度问题 timetable scheduling

问题(Q): 如何安排考试时间表,使得没有学生需要在同一时间参加两门(或更多)的考试?
答案(A): 需要3个考试时间段。
建模方法(Argument):
- 将每门科目表示为图 的一个顶点。
- 如果两门科目有共同的学生,则在对应的顶点之间画一条边。
- 通过这种方式,我们得到了一个图,其中顶点代表科目,边代表科目间的冲突(即不能同时安排的科目)。
- 这个问题的目标是用最少的颜色对所有顶点进行着色,使得任何两个有边相连的顶点(冲突的科目)有不同的颜色。
- 在这个模型中,一个颜色代表一个时间段,所以着色问题转化为了时间段的分配问题。
- 需要的最小颜色数,即图的色数 ,表示了所需的最少时间段数。
- 在这个具体的例子中,色数 等于3,意味着我们需要3个不同的时间段来安排所有考试,以保证没有学生需要同时参加两门或更多的考试。
平面图 planar graphs
定义
如果它可以嵌入到一个平面中而没有边相交,那么这个图是平面的(planar)。简单来说,如果你能将一个图画在纸上而没有任何线条交叉,那么这个图就是平面图。
定理
如果图是平面的,那么它可以被嵌入到平面中,所有的边都是直线,并且没有自相交。
这个定理说明了平面图不仅可以被绘制出来而且没有边的交叉,还可以做到所有边都是直线而不需要弯曲。
注
这个概念及其相关算法对于VLSI(Very Large Scale Integration,超大规模集成电路)和数据可视化都极其重要。在VLSI中,设计印刷电路板时,需要确保线路不交叉以避免短路;在数据可视化中,平面图用来清晰表示复杂信息而避免视觉混乱。
非平面性的相关定理 testing for nonplanarity
子图的非平面性性质
如果一个图 作为一个子图包含一个非平面图,那么 本身也是非平面的。这意味着,如果在一个大的图中能找到一个不能画在平面上而边不相交的小图,那么这个大图也不能在平面上画出来而边不相交。
非平面的关键判定细分
边细分(Edge subdivision)
边细分是指在图的一条边中插入一些新顶点,这些新顶点的度(与其相连的边数)为2。在PPT中的例子中,原图的一条边被细分,加入了两个新顶点,使得原先直接相连的两个顶点现在通过两条边和一个新顶点相连。这种操作后得到的图称为原图的一个细分(subdivision)。
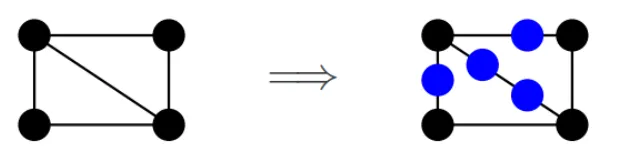
如果一个图是非平面的,那么它必须包含一个 完全图 或 的细分。
这是库拉托夫斯基定理的一部分,是平面图理论中的一个基本结果,用于确定一个图是否可以画在一个平面上而没有边相交。
简而言之,如果在一个图中找不到这两种特定图形的细分,那么这个图就是平面的。
其他定理
- 所有的完全图 都是非平面的。因为 都是它们的子图,而 是非平面的。
- 所有的完全图 都是非平面的。因为 都是它们的子图,而 是非平面的。
如果图有5个或更多顶点,并且所有顶点都互相连接(),或者如果图是一个具有至少3个顶点的完全二分图(),那么这个图是非平面的。
寻找细分的策略 strategy for finding a subdivision
策略1
为了证明图 包含图 的一个细分作为子图(通常为了证明含 等图的细分以证明不具有平面性),可以使用以下步骤:
- 从图 开始。
- 多次执行以下操作:
- 细分一条边(在边上增加一个顶点,将一条边分为两条边)。
- 添加一个顶点(增加一个新的顶点到图中)。
- 添加一条边(在两个顶点之间增加一条边)。
- 得到图 。
注
- 每个操作都会增加顶点集 或边集 的大小。
- 可以首先完成某种操作。如,你可以先细分所有需要细分的边,再添加所有需要添加的顶点,最后添加所有需要添加的边。
这个策略有助于系统地构造出一个包含 的细分的图 ,这对于证明某些图论问题是非常有用的,例如证明一个图是非平面的。通过一系列的边细分 。这个过程在图的绘制、网络设计等方面非常重要,特别是在需要证明某个图不能被简化为更简单形式时。
策略2
为了证明图 包含图 的一个细分作为子图(通常为了证明含 等图的细分以证明不具有平面性),可以使用以下步骤:
- 从图 开始。
- 多次执行以下操作:
- 删除一条边(从图中移除一条边)。
- 删除一个顶点(以及与之相连的所有边)。
- 替换一个度为2的顶点与一个连接它的邻居的边(收缩一个顶点)。
- 得到图 。
注
- 每个操作都会减少顶点集 或边集 的大小。
- 可以首先完成某种操作。如,你可以先先删除所有需要删除的边,再删除所有需要删除的顶点,最后收缩所有需要收缩的顶点。
这个策略是一个逆向过程,与策略 I 相反。它从大图 开始,通过删除边和顶点以及收缩顶点的操作来简化图,最终得到一个子图 的细分。这种方法在图论中用于证明图 包含图 的细分,这对于解决某些图的问题非常有用,尤其是在证明图的非平面性或在求解图的最小化问题时。通过这种方式,可以显示一个复杂的图包含一个更简单图形的细分,这对于图的分类和识别特定的图属性是非常重要的。
不变性
What does not change when performing the operations?
当执行图的细分或相关操作时(如删除顶点、删除边、替换顶点等),有一个关键特征是不会改变的,那就是图的平面性(planarity)。如果原始图是平面的,那么通过这些操作得到的细分图同样也是平面的;反之,如果原始图是非平面的,无论如何细分或修改,它仍然是非平面的。
除了平面性,还有一个属性在这些操作中不会改变,那就是图的连通性模式。例如,如果原始图在细分前是连通的,那么在细分后也应该保持连通。同样,如果原始图中有特定数量的连通分支,那么在细分后也会保持相同的连通分支数量。
在图的细分操作中,这些不变性是很重要的,因为它们可以帮助确定是否可能通过细分原始图来获得另一个特定的图。如果在进行细分操作后,我们得到的图与特定的图在这些基本属性上不一致,那么我们可以断定原始图不包含作为子图的那个特定的图的细分。
本文作者:Jeff Wu
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!