• Propositional Logic, informally
• Propositional Logic, formally
• CNF and DNF Revisited
• Beyond Propositional Logic

命题逻辑 非正式 Propositional Logic, informally

命题定义 Definition

命题（或句子）是一种陈述句；其内容可以是真也可以是假。

逻辑连接词 Logical connectives

逻辑连接词用来将命题连接起来，构建更大的、复合的命题。

逻辑连接词包括"and"（和）、"or"（或）、"not"（不是）、"if...then..."（如果...那么...）等，用于建立逻辑上更复杂的陈述。通过逻辑连接词组合的命题的真假取决于它们所连接的各个简单命题的真假以及这些逻辑连接词本身所代表的意义。

复合命题 Compound propositions

复合命题的真理值取决于它的组成部分（原子命题）的真理值。

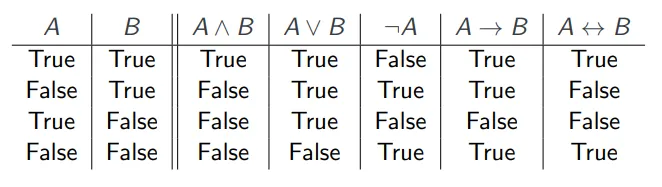
恒真式、矛盾和偶然性 Tautologies, Contradictions and Contingencies

• 一个命题如果永远为真，就是恒真式（tautology）。
• 一个命题如果永远为假，就是矛盾（contradiction）。
• 一个命题如果既不是恒真式也不是矛盾，就是偶然性（contingency）。
• 如果一个命题不是矛盾，它就是可满足的（satisfiable）。

恒真式是指无论在什么情况下都为真的命题。矛盾是指一个命题和它自身否定同时为真，这在逻辑上是不可能的，因此这样的命题永远是假的。偶然性是指一个命题在某些情况下为真，在其他情况下为假。可满足性指的是至少在一种情况下命题为真。

逻辑等价 Logical equivalence

如果两个命题对于其原子命题的相同真值都为真，那么这两个命题是逻辑等价的。逻辑等价意味着两个命题在逻辑上是不可区分的，它们要么同时为真，要么同时为假。在逻辑表达和推理中，逻辑等价的命题可以互换使用。

蕴涵与有效性 Entailment and Validity

一个论证由一组称为前提的命题和一个称为结论的陈述句组成。

前提：

• Frank took the Ford or the Toyota.（Frank开了福特或者丰田。）
• If Frank took the Ford he will be late.（如果Frank开了福特，他会迟到。）
• Frank is not late.（Frank没有迟到。）

结论：

• Frank took the Toyota.（Frank开了丰田。）

在这个例子中，结论是基于前提合理推导出来的。第一个前提提供了两种可能性，第二个前提提供了一种条件性的结果，第三个前提是一个事实陈述。结合这些前提，我们可以推导出结论，即Frank开了丰田。这个结论是有效的，因为它符合所有前提。

一个论证是有效的，如果结论在所有前提都为真的情况下为真。因此，如果我们相信前提，我们也应该相信结论。（注：当其中一个前提是假的时候我们不关心会发生什么。）

其他表达相同含义的说法：

• 结论逻辑上从前提中得出。（The conclusion logically follows from the premises.）
• 结论是前提的逻辑后果。（The conclusion is a logical consequence of the premises.）
• 前提蕴涵结论。（The premises entail the conclusion.）

有效性是逻辑推理中的关键概念，它确保了如果我们接受前提，那么由这些前提推理出的结论也应当被接受。这与前提的真实性无关；即使前提是假的，但如果逻辑结构是正确的，那么论证就是有效的。在逻辑分析中，我们只关注论证的形式结构，而不是前提的实际内容。

命题逻辑 正式 Propositional Logic, formally

语法与语义 Syntax vs Semantics

逻辑正式定义的第一步是区分语法和语义。语法是指事物如何被书写，即定义了一个公式。语义是指事物的含义，即一个公式为何为“真”。

语法：合成公式 Syntax: Well-formed formulas

有命题集合：$PROP=\{p, q, r...\}$

考虑字母表：

⊤代表"真"（tautology），在任何可能的情况下都是真的。

⊥代表"假"（contradiction），在任何可能的情况下都是假的。

PROP 上的合式公式（wffs）是 Σ 上的最小字集，满足以下条件：

• ⊤, ⊥ 以及 PROP 的所有元素都是 wffs。
• 如果 $φ$ 是一个 wff，那么 $¬φ$ 也是一个 wff。
• 如果 $φ$ 和 $ψ$ 都是 wffs，那么 $(φ ∧ ψ)$, $(φ ∨ ψ)$, $(φ → ψ)$, 和 $(φ ↔ ψ)$ 也都是 wffs。

语法：约定 Syntax: Conventions

为了帮助提高可读性，一些约定和绑定规则将被使用：

• 如果没有歧义，可以省略括号（例如 p ∧ q）。
• ¬ 比 ∧ 和 ∨ 绑定得更紧密，而 ∧ 和 ∨ 比 $→$ 和 $↔$ 绑定得更紧密（例如 p ∧ q → r 代替 ((p ∧ q) → r)）。
• ∧ 和 ∨ 默认向左结合（例如 p ∨ q ∨ r 代替 ((p ∨ q) ∨ r)）。

其他在本门课中中很少使用或假定的约定：

• ′ 或 : 代替 ¬。
• • 代替 ∨。
• . 或紧邻代替 ∧。
• ∧ 比 ∨ 绑定得更紧密。
• $→$ 和 $↔$ 默认向右结合（例如 p → q → r 代替 (p → (q → r))）。

语法：解析树 Syntax: Parse trees

合式公式（以及其他由语法定义的句法结构）的结构可以用解析树来展示。

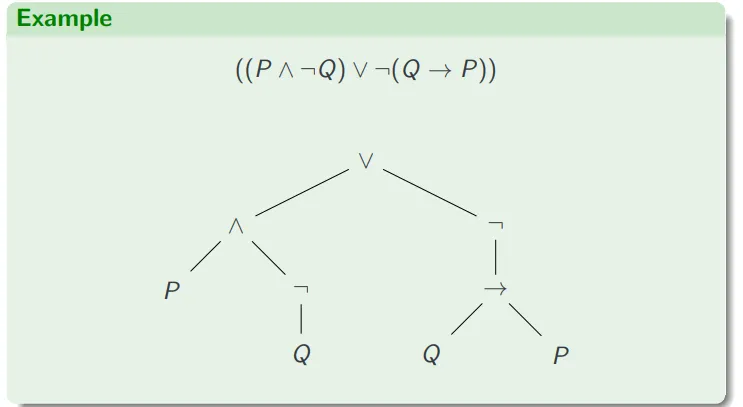
形式化地，我们可以按照以下方式定义解析树： 一个解析树可以是：

• （B）一个包含 ⊤ 的节点；
• （B）一个包含 ⊥ 的节点；
• （B）一个包含命题变量的节点；
• （R）一个包含 ¬ 和单个解析树子节点的节点；
• （R）一个包含 ∧ 和两个解析树子节点的节点；
• （R）一个包含 ∨ 和两个解析树子节点的节点；
• （R）一个包含 → 和两个解析树子节点的节点；
• （R）一个包含 $↔$ 和两个解析树子节点的节点。

这里的（B）代表基本情况，而（R）代表递归规则。基本情况意味着一个节点可以直接表示一个命题逻辑的常量或变量，而递归规则意味着可以从一个或两个子节点构建更复杂的逻辑结构。解析树的每个节点都对应一个逻辑运算符或操作数，树的结构显示了复合命题中不同部分之间的关系。

语义：布尔代数 Semantics: Boolean Algebras

回顾两元素布尔代数 𝔹 = {true, false} = {⊤, ⊥} = {1, 0}，以及操作 !, &&, ||。

定义派生布尔函数 $⇝$ 和 $↭$：

语义：真值赋值 Semantics: Truth valuations

真值赋值（也称为真值评价）是一个函数 $v:Prop→B$.

我们可以按照如下方式将真值赋值 v 扩展到所有命题逻辑的合式公式 (wffs)：

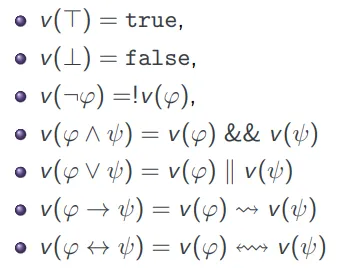
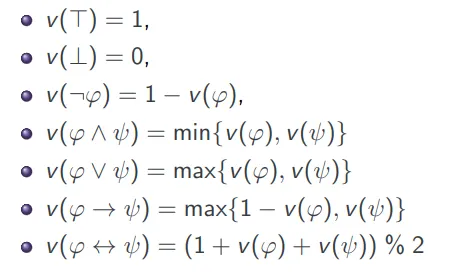
语义：真值表 Semantics: Truth tables

每个真值赋值 —— 即为 Prop 的元素赋予 T/F —— 都对应一行。每个子公式对应一列。

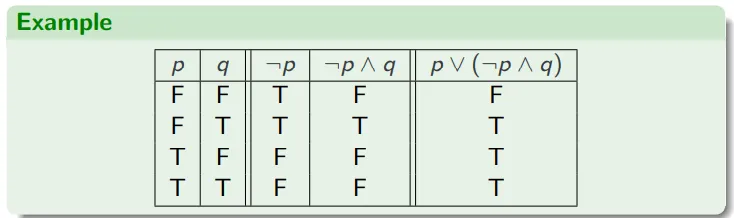
可满足性，有效性，等价性 Satisfiability, Validity and Equivalence

一个公式 φ：

• 如果存在某个真值赋值 v 使得 v(φ) = true，则称 φ 是可满足的（φ satisfies v）。
• 如果对所有的真值赋值 v，v(φ) = true，则称 φ 是一个重言式（tautology）。或者也可以说是个恒等式。
• 如果对所有的真值赋值 v，v(φ) = false，则称 φ 是不可满足的（unsatisfiable），或者说是一个矛盾（contradiction）。

逻辑等价 Logical equivalence

两个公式 φ 和 ψ 被认为是逻辑等价的，记为 φ ≡ ψ，如果对所有真值赋值 v，v(φ) = v(ψ)。

理论和蕴含 Theories and entailment

一组公式（Formula）的集合被称为理论（Theory）。

如果一个真值赋值$v(t) = true$ 对所有的 $t \in T$ 都成立，我们说这个真值赋值v满足理论T。

如果一个公式 $φ$ 使得 $v(φ) = true$ 对于所有的满足T的真值赋值v都成立，那么我们说理论T蕴含一个公式 $φ$ ，记作 $T⊨φ$。