目录
Lecture 7: Relations
- Definition and Examples
- Binary Relations
- Properties of Binary Relations
- Functions
定义与例子 Definition and Examples
关系 Relations
n元关系(n-ary relation)是n个集合的笛卡尔积的子集,记作:
特殊地,当 时,我们称之为二元关系(binary relation),记作:
并且展示相关联的数对时,写作:
笛卡尔积的结果集合 ,称之为 的定义域(domain)。如果关系 定义域在 上,我们就说 是 上的关系。
例子


在这个关系中,enrolment显然是学生与课程的对(pair),但应当不是笛卡尔积的全集(因为不太可能每一名学生都会修掉所有的课)。

定义关系 Defining Relations
有以下几种方式定义一个关系 :
- 通过明确地列举相关的k元组来定义:这里的k元组指的是在二元关系的情况下的有序对。
- 通过识别大的笛卡尔积内部的相关元组的属性来定义:这意味着关系可以通过满足特定关系的元组的等式/不等式/关系式等描述。
- 通过其他关系构建定义:例如通过交集,并集,补集等。


二元关系 Binary relations
在集合S和T之间的二元关系是 的子集,即有序对的集合。
特殊的二元关系例子:
- 恒等关系(Identity):这是对角线关系,也称等价琯溪,定义为 ,其中每个元素与自身形成对。
- 空关系(Empty):不包含任何元素的关系,记作 。
- 全域关系(Universal):包含所有可能有序对的关系,定义为 。
定义二元关系的方法 Definition binary relations
基于集合定义 Set-based definitions
参考:定义关系部分。
矩阵描绘 Matrix representation

图像描述 Graphical representation
集合图表示
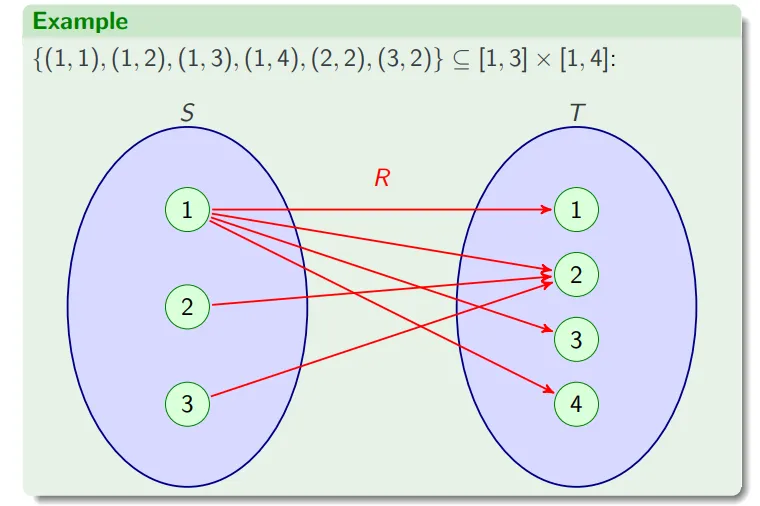
有向图表示
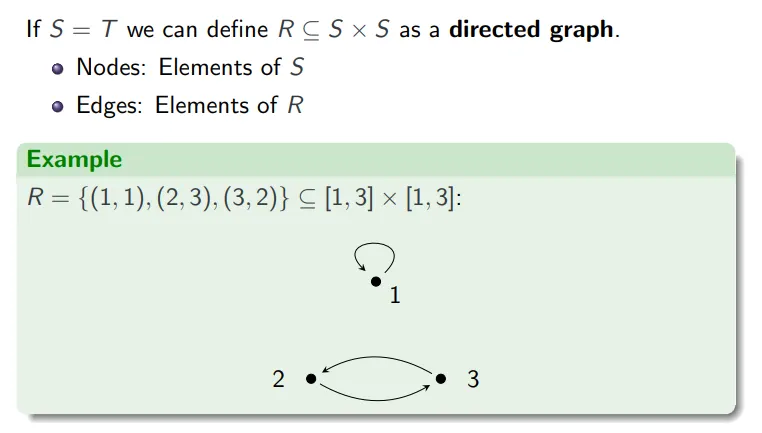
二元关系操作 Operations for binary relations
逆关系 Converse
如果有一个关系 ,那么它的逆关系 定义为:
这意味着在逆关系中,每个有序对的元素顺序会被反转。并且,显然有:
复合关系 Composition
如果 并且 ,那么它们的符合关系 定义为:
复合关系意味着从集合S到U存在一个通过集合T中介的关系路径。
关系映像 Relational images
想象一下你在学校的学生和他们参加的俱乐部之间有一个列表,这个列表就是一个关系,它告诉你哪个学生参加了哪个俱乐部。
现在,如果你想知道某个特定学生参加了哪些俱乐部,你就会查找与这个学生相关的所有俱乐部,这就是关系映像。就像你拿着学生的名字去映射找出他们参加的所有俱乐部。
反过来,如果你手头有一个俱乐部的名单,你想找出所有参加这个特定俱乐部的学生,你就会查找与这个俱乐部相关的所有学生,这就是关系预映像。这就像是你从俱乐部的角度出发,反向映射回去找到所有相关的学生。
简单来说,关系映像就是从一个集合(比如学生)出发,找到与它们相关联的另一个集合(比如俱乐部)中的成员。而关系预映像则是反过来的操作。
给定关系 ,,并且 。
关系映像 Relational image
关系映像 被定义为:
简而言之, 包含了所有与集合A中的元素通过关系R相关联的T中的元素。
关系预映像 Relational pre-image
关系预映像 被定义为:
简而言之, 包含了所有能够通过关系R找到与B中元素相对应的S中的元素。
二元关系的性质 Properties of Binary Relations
-
函数式(Fun) functional:对于每个 中的元素 ,在关系 中至多与一个 中的元素 关联。也就是说每个 都至多映射到一个 。
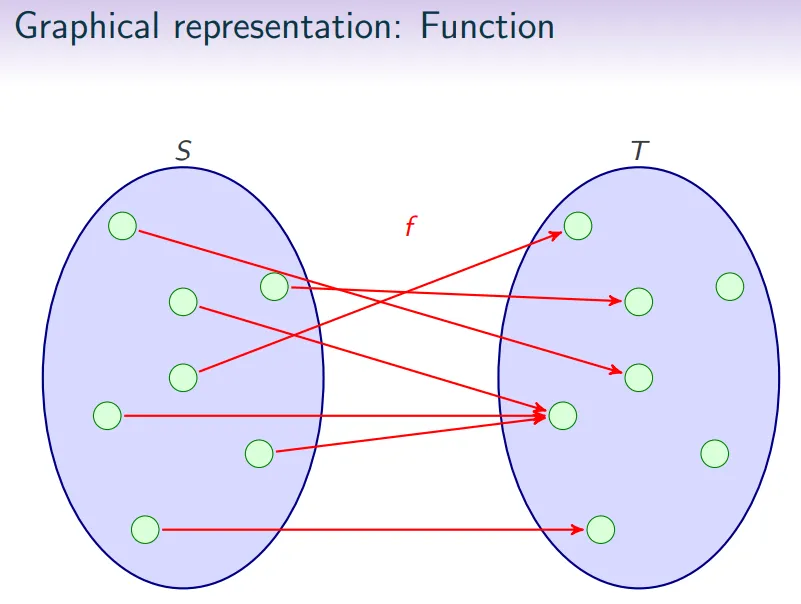
-
全域性(Tot) total:对于每个 中的元素 ,在关系 中至少与一个 中的元素 关联。也就是说每个 都至少映射到一个 。
-
单射(Inj) injective:对于每个 中的元素 ,在关系 中至多与一个 中的元素 关联。也就是说不同的 映射到不同的 。
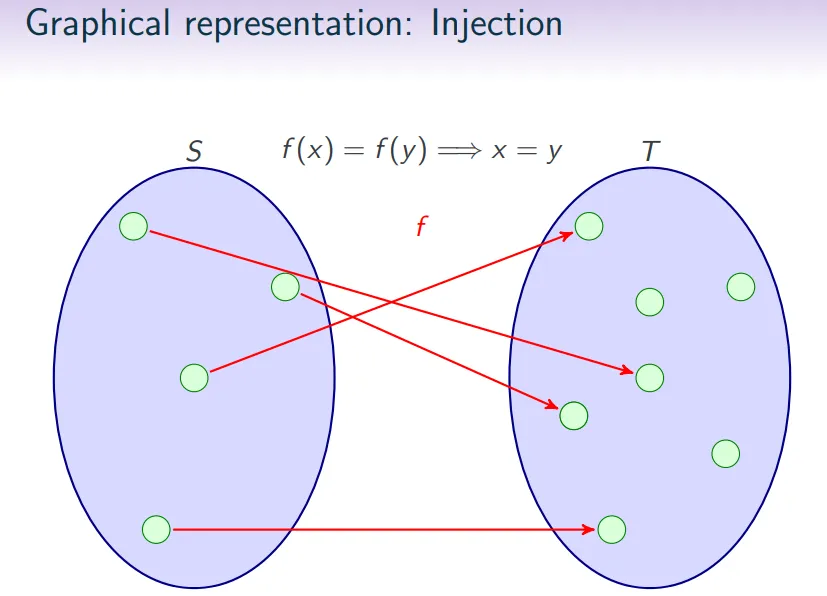
-
满射(Sur) surjective:对于每个 中的元素 ,在关系 中至少与一个 中的元素 关联。也就是说 中的每个元素都是某个 的映射。
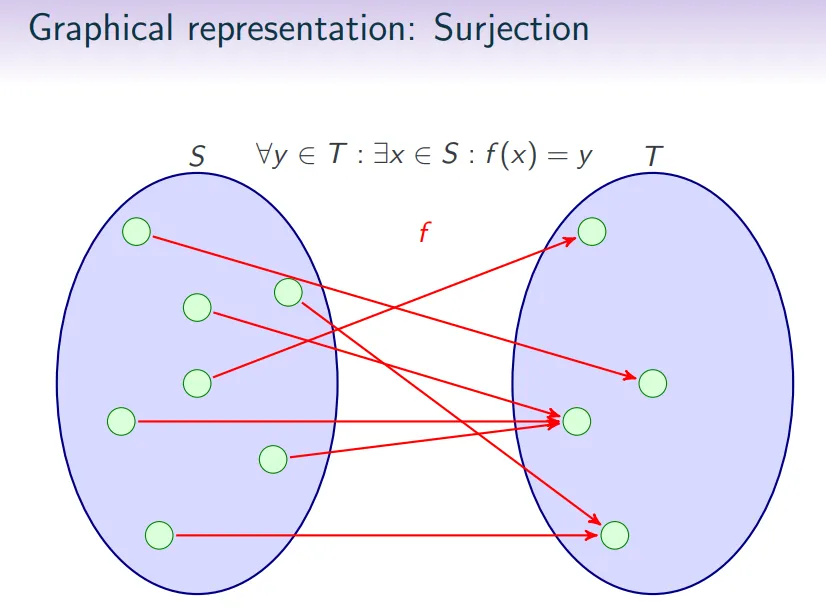
-
双射(Bij) bijective:关系 同时满足单射和满射。也就是说, 到 的映射是一对一的(每个 只能映射到一个独特的 ),并且是覆盖的( 中的每一个 都被 中的某个 映射到)。
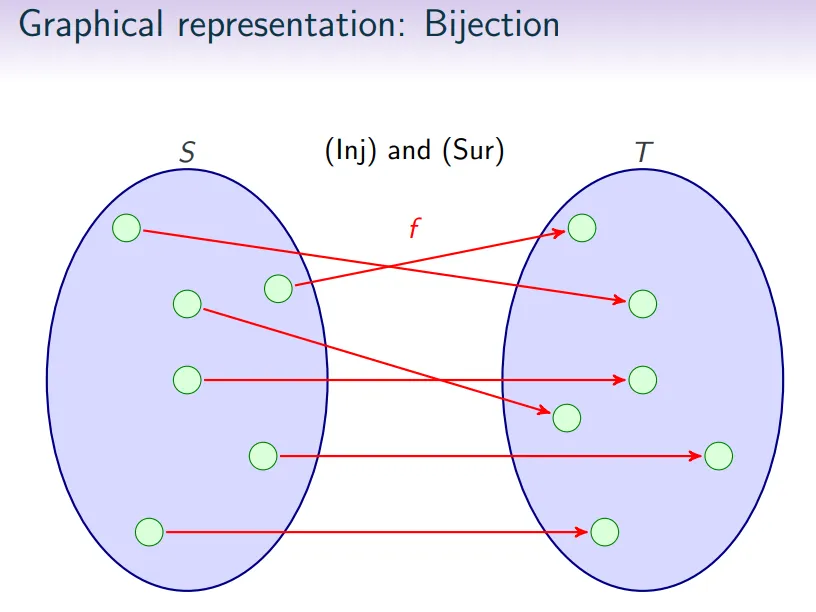
同一集合上的二元关系性质 Properties of Binary Relations
- 自反性(R)reflexive:对于集合 中的所有元素 ,都有 。也就是说,每个元素都与自己本身在关系 中有关联。
- 反自反性(AR)antireflexive:对于集合 中的所有元素 ,都有 。也就是说,没有任何元素与自己本身在关系 中有关联。
- 对称性(S)symmetric:如果有序对 ,且 。
- 反对称性(AS)antisymmetric:如果有序对 和 都在 中,必须有 。
- 传递性(T)transitive:如果有序对 和 都属于关系 ,那么 。
如果某关系具有该性质,意味着这些性质是对关系中的所有元素都成立的。
其中,S,AS,T是条件语句,如果没有任何元素满足“如果”部分的条件,那么属性被认为是成立的。例如,如果在关系中不存在任何两个不同元素 使得 和 同时存在,那么该关系就被视为反对称的。
性质的交互 Interaction of Properties
一个关系可以同时是对称的和反对称的。这种情况发生在关系 仅由形如 的有序对组成时,也就是说,除了自反元素之外没有其他元素。在这种情况下,每个元素与自己相关联,但没有不同的元素 使得 和 同时在 中。
关系不能同时是自反的和反自反的,除非集合 是空集。这是因为自反性要求集合 中每个元素与自己相关联,而反自反性要求没有任何元素与自己相关联,这两个定义是相互矛盾的。
不具有自反性(nonreflexive)或不具有对称性(nonsymmetric)的关系,不等同于反自反的(antireflexive/irreflexive)或反对称的(antisymmetric)关系。这是关系属性的一个重要区别,因为“不具有某属性”(如不自反或不对称)并不一定意味着它具有对应的“反属性”(如反自反或反对称)。
例如,一个关系,如果它对某些元素是自反的,而对其他元素则不是自反的,那么该关系既不是自反的也不是反自反的。
数学函数 Functions
一个函数 ,是从集合 到集合 的一个二元关系 ,且满足函数式(Fun)和全域性(Tot)两个属性。也就是说,对于集合 中的每一个元素 ,都有且只有一个元素 在集合 中与之关联。
如果 唯一关联 ,我们用 来表示 这个唯一关联的 。
我们用函数集 表示从 到 的所有可能的函数的集合。
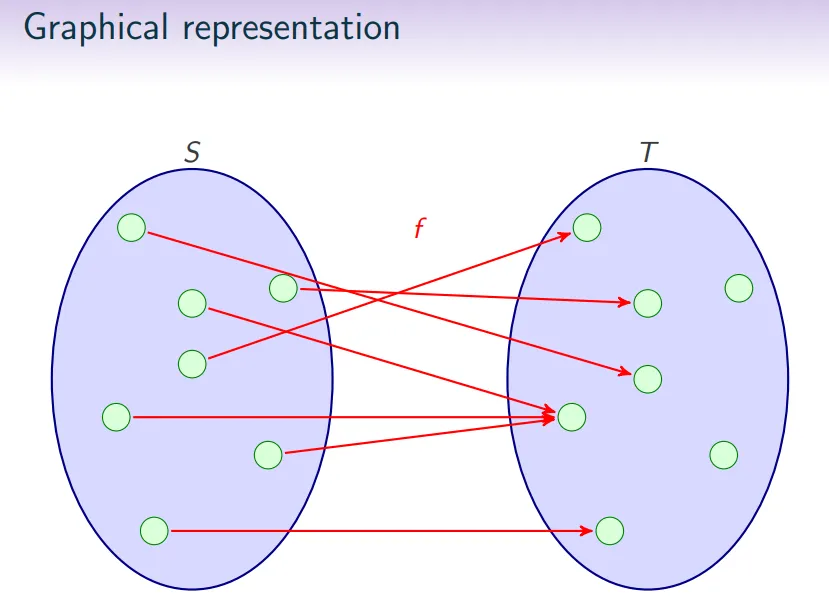
术语
- 定义域(domain),包含所有可能的输入,即集合 。
- 上域(co-domain),包含所有可能的输出,即集合 。
- 像(image),即值域(range),是函数 的实际所有输出,为 的子集。
符号
- 定义域:
- 上域:
- 像:,也可写作
要点
定义域,上域,方法,三者完全相同的,才能认为是相同的函数。不同的定义域/上域,会影响函数的性质和应用。
当函数 同时满足单射和满射(即双射,或称一一对应函数)时, 关系 才能也是一个函数。
双射的性质 Properties of bijections
- 如果 和 是双射,那么它们的逆函数也是双射的。
- 函数 和 的复合 也是双射。
- 函数 与它的逆函数 的复合等于在 上的恒等关系,记作 ,它包含所有形如 的元素对,其中 。
- 逆函数 与函数 的符合等于在 上的恒等关系,记作 ,它包含所有形如 的元素对,其中 。
最后两个性质实际上定义了双射函数的逆函数关系,也就是说,你可以通过 找到 中的每个元素的原像,反过来通过 找到 中的每个元素的原像,没有遗漏也没有重复。

本文作者:Jeff Wu
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!