Lecture 8: Equivalence Relations and Partial Orders

• Equivalence Relations
• Partial Orders

等价关系 Equivalence relations

等价关系是一种捕捉“相等”这一概念的二元关系，它必须满足以下三个属性：

• 自反性。每个对象都应当与自身相等。$(x,x) \in R$
• 对称性。如果 $(x,y) \in R$，那么 $(y,x) \in R$
• 传递性。如果$(x,y) \in R, (y,z) \in R$，那么 $(x,z) \in R$

根据定义，一个二元关系 $R$ 是集合 $S$上的等价关系，当且仅当它满足自反性（R）、对称性（S）和传递性（T）。

等价类 Equivalence Classes

假设 $R \subseteq S \times S$ 是一个等价关系。

集合 $S$ 中的元素 $s$ 的等价类（记作 $[s]$）是所有与 $s$ 相等（根据关系 $R$）的元素的集合。形式上，有：

等价类的概念指，如果你取了集合 $S$ 中的任意一个元素 $s$ 并且找到了所有与它相等的元素 $t$，那么这些元素 $t$ 形成的集合就是 $s$ 的等价类。

$s$ 和 $t$ 在关系 $R$ 下相等当且仅当它们属于同一个等价类，即 $[s]=[t]$。

划分 Partitions

集合 $S$ 的划分是一组集合 $S_1,S_2,...S_k$，满足：

• 对于任意不相同的 $i,j$，均有 $S_i \cap S_j=\empty$，即任意两集合不相交。
• 集合 $S$ 是这些集合的并集，即 $S=S_1 \cup S_2 \cup ... \cup S_k$。

如果你有集合 $S = S_1 \cup ... \cup S_k$，那么划分实际上也定义了一个等价关系。每个元素都有属于自己的一个子集 $S_i$。如果想定义两个元素等价，我们可以定义等价关系 $\sim \subseteq S \times S$ 上如下：

• $s\sim t$ 当且仅当 $s$ 和 $t$ 属于同一个子集 $S_i$。

该定义表示 $s$ 与 $t$ 等价。

偏序集 Partial Order

如果一个关系 $\preceq$ 在集合 $S$ 上是偏序地，需要满足以下三个条件：

• 自反性。
• 反对称性。
• 传递性。

集合 $S$ 与偏序关系 $\preceq$ 一起构成一个偏序集，简称为poset。

以下是一些常见的偏序集例子：

• $(Z, \le)$
• $(N, |)$

哈斯图 Hasse diagram

它是一种表示有限偏序集的图形工具。

• 每个节点代表偏序集 $S$ 中的一个元素。
• 如果 $x \prec y$，并且中间没有元素 $z$ 使得 $x \prec z \prec y$，那么在哈斯图中从 $x$ 向上画一条到 $y$ 的边。

元素排序 Ordering Concepts

在偏序集 $(S, \preceq)$ 中，一些基本概念如下：

• 极小元素 Minimal element：在偏序集 $(S, \preceq)$ 中，如果不存在另一个不同的元素 $y$ 满足 $y \preceq x$，那么称 $x$ 为极小元素。
• 极大元素 Maximal element：在偏序集 $(S, \preceq)$ 中，如果不存在另一个不同的元素 $y$ 满足 $x \preceq y$，那么称 $x$ 为极大元素。
• 最小元素 Minimum element：如果对于所有 $y \in S$，都有 $x \preceq y$，那么 $x$ 被称为最小元素。
• 最大元素 Maximum element：如果对于所有 $y \in S$，都有 $y \preceq x$，那么 $x$ 被称为最大元素。

• 上界 upper bound：如果 $x$ 满足对集合 $A$ 中的所有元素 $a$，都有 $a \preceq x$，那么 $x$ 就是 $A$ 的一个上界。
• 下界 lower bound：如果 $x$ 满足对集合 $A$ 中的所有元素 $a$，都有 $x \preceq a$，那么 $x$ 就是 $A$ 的一个下界。
• 上界集合 set of upper bounds：$ub(A)=\{x: a \preceq x \text{ for all } a \in A\}$
• 下界集合 seet of lower bounds：$lb(A)=\{x: x \preceq a \text{ for all } a \in A\}$
• 最小上界 least upper bound：如果存在，集合 $A$ 的最小上界是上界集合中的最小元素，记作 $lub(A)$。也称上确界。
• 最大下界 greatest lower bound：如果存在，集合 $A$ 的最大下界是下界集合中的最大元素，记作 $glb(A)$。也称下确界。

• 格 lattice：对于偏序集 $S, \preceq$，如果对于任意两个元素 $x,y \in S$，它们的上确界 $lub(S)$ 和下确界 $glb(S)$ 都存在，那么称该偏序集为一个格。
• 完备格 complete lattice：对于偏序集 $S, \preceq$，如果对于 $S$ 的任意子集 $A$，它的上确界 $lub(A)$ 和下确界 $glb(A)$ 也都存在，那么称该偏序集为一个完备格。

全序 Total orders

全序是一种特殊的偏序关系，它除了满足偏序的基本条件（自反性、反对称性、传递性）之外，还满足线性性（Linearity）。这意味着集合中的任何两个元素都可以进行比较：

• 对于所有的 $x,y$，要么出现 $x \le y$，要么出现 $y \le x$。（如果 $x = y$ 则两者都成立）

在有限集合上，所有的全序关系都是“同构”的。这意味着在有限集合上的任意两个全序关系，你总能找到一种方式将一个全序集映射到另一个全序集，保持其顺序结构不变。

在无限集合上，存在多种全序关系的可能性。这表示无限集合上的全序可以有多种不同的结构，不能简单地通过同构关系进行映射。

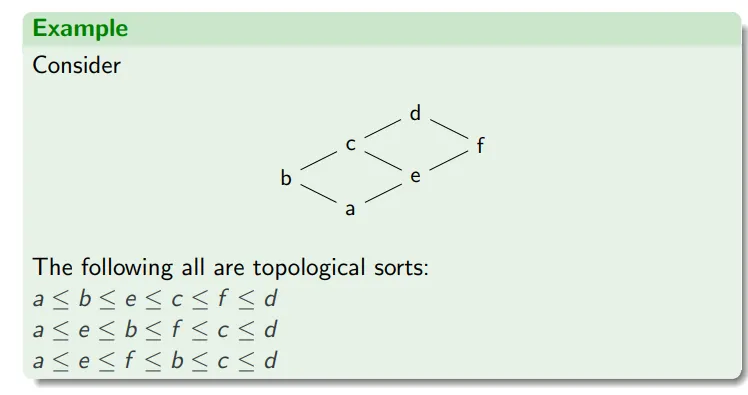
拓扑排序 Topological Sort

对于一个偏序集 $(S, \preceq)$，任何与偏序 $\preceq$一致的全序 $\le$ 都成为拓扑排序。这意味着在偏序关系中如果 $a \preceq b$，那么在拓扑排序中一定有 $a \le b$。

良序集 Well-Ordered Sets

良序集是一个偏序集，其中每个子集都有一个最小元素。良序集不要求有最大元素。

自然数集N是一个良序集，每个子集都一定有一个最小元素。

良序集是一个重要的数学工具，用于证明程序的终止。因为在良序集中，你可以总是找到一个最小的元素，所以在迭代或递归的情况下，你可以保证每个步骤都是向终止条件靠近，而不是无限进行下去。这在证明算法正确性和计算复杂性时非常有用。

笛卡尔积乘积序 Orders for Cartesian products

给定两个偏序集 $(S, \preceq_S)$ 和 $(T, \preceq_T)$，可以定义它们的乘积序如下：

对于 $S \times T$ 中的任意两个元素 $(s,t)$ 和 $(s',t')$，当且仅当 $s \preceq_S s'$，并且 $t \preceq_T t'$ 时，有：

乘积序有以下特点：

• 没有隐含的权重。这意味着在比较两个元素时，$S$ 和 $T$ 中的元素被平等对待。
• 没有对任何组成部分的偏见。乘积序中没有一个方向比另一个更重要。
• 通常，乘积序只是一个偏序，即使是将全序结合起来也是如此。也就是说，即使 $S$ 和 $T$ 上各自的序是全序，它们的乘积也不一定是全序。

乘积序是理解多维数据结构中元素顺序的重要概念，例如，在数据库、多维数组或是在编程语言中处理多个有序集合时非常有用。它允许我们从多个维度组合和比较数据点。

笛卡尔积字典序 Orders for Cartesian lexicographic

给定两个偏序集 $(S, \preceq_S)$ 和 $(T, \preceq_T)$，可以定义它们的字典序如下：

对于 $S \times T$ 中的任意两个元素 $(s,t)$ 和 $(s',t')$，当 $s \preceq_S s'$，或者 $s=s', t \preceq_T t'$ 时，有：

这意味着先比较第一个元素，如果第一个元素相同，再比较第二个元素。

字典序有以下特点：

• 没有隐含的权重：即没有一个组件比另一个更重要。
• 当组合两个全序时，会给出全序。
• 可以扩展到单词：这意味着可以用来对字符串数组进行排序，比如在字典中排序单词一样。
• 不适合枚举。

字典序是一种重要的序，因为它允许我们对组合数据进行有序排列，这在数据结构、数据库索引以及编程语言中处理字符串时特别有用。它在数学和计算机科学中有广泛的应用。